题目内容
2.$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=$\frac{4}{5}$的正整数解有( )组.| A. | 0 | B. | 8 | C. | 12 | D. | 16 |
分析 从x,y,z是正整数入手,确定它们倒数的取值范围,从而确定x,y的取值,进而得出z的取值.
解答 解:∵x,y,z是正整数,并且$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$=$\frac{4}{5}$<1
∴x,y,z都>1,不妨设1<x≤y≤z,
∴$\frac{1}{x}$≥$\frac{1}{y}$≥$\frac{1}{z}$,于是$\frac{1}{x}$<$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$≤$\frac{1}{x}$+$\frac{1}{x}$+$\frac{1}{x}$=$\frac{3}{x}$,即$\frac{1}{x}$<$\frac{4}{5}$≤$\frac{3}{x}$,
∴$\frac{5}{4}$<x≤$\frac{15}{4}$,可确定x=2或3,
当x=2时,得$\frac{1}{y}$<$\frac{1}{y}$+$\frac{1}{z}$=$\frac{4}{5}$-$\frac{1}{2}$=$\frac{3}{10}$≤$\frac{1}{y}$+$\frac{1}{y}$=$\frac{2}{y}$,
即$\frac{1}{y}$<$\frac{3}{10}$≤$\frac{2}{y}$,
∴$\frac{10}{3}$<y≤$\frac{20}{3}$,可知y=4或5或6.
当x=3时,由$\frac{1}{y}$+$\frac{1}{z}$=$\frac{4}{5}$-$\frac{1}{3}$=$\frac{7}{15}$得:$\frac{1}{y}$<$\frac{1}{y}$+$\frac{1}{z}$=$\frac{7}{15}$≤$\frac{1}{y}$+$\frac{1}{y}$=$\frac{2}{y}$,
即$\frac{1}{y}$<$\frac{7}{15}$≤$\frac{2}{y}$,
∴$\frac{15}{7}$<y≤$\frac{30}{7}$,可知y=3或4,
当x=2,y=4时,z=20;
当x=2,y=5时,z=10;
当x=2,y=6时,z=7.5(舍去);
当x=3,y=3时,z=7.5(舍去);
当x=3,y=4时,z=$\frac{60}{13}$(舍去);
因此,当1<x≤y≤z时,(x,y,z)为(2,4,20),(2,5,10),共2组,
由于x,y,z在方程中地位平等,所以可得12组解为(2,4,20),(2,20,4),(4,2,20),(4,20,2),(20,2,4),(20,4,2),(2,5,10),(2,10,5),(5,2,10),(5,10,2),(10,2,5),(10,5,2).
故选:C.
点评 此题主要考查了非一次不定方程(组),分式方程整数根的求法,以及利用极值法确定未知数的范围,题目综合性较强.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
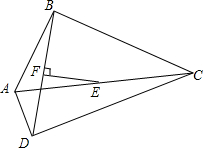 如图,在四边形ABCD中,E、F分别是AC、BD的中点,EF⊥BD,点F为垂足,∠ADC=90°.求∠ABC的度数.
如图,在四边形ABCD中,E、F分别是AC、BD的中点,EF⊥BD,点F为垂足,∠ADC=90°.求∠ABC的度数.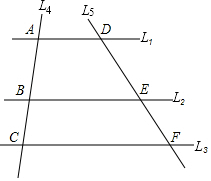 直线L1∥L2∥L3,直线L4被L1,L2,L3所截,其中截得的两条线段分别为AB,BC.L5是另外一条被L1,L2,L3所截的直线,其中截得的两条线段分别为DE,EF.小明通过测量得出AB≈1.89cm,BC≈3.80cm,DE≈2.02cm,那么EF约等于4.06cm.
直线L1∥L2∥L3,直线L4被L1,L2,L3所截,其中截得的两条线段分别为AB,BC.L5是另外一条被L1,L2,L3所截的直线,其中截得的两条线段分别为DE,EF.小明通过测量得出AB≈1.89cm,BC≈3.80cm,DE≈2.02cm,那么EF约等于4.06cm.
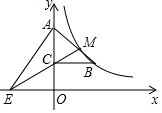 如图,反比例函数y=$\frac{k}{x}$的图象经过Rt△ABC斜边AB的中点M 及顶点B,点C在y轴正半轴上,连结MC并延长与x轴交于点E.
如图,反比例函数y=$\frac{k}{x}$的图象经过Rt△ABC斜边AB的中点M 及顶点B,点C在y轴正半轴上,连结MC并延长与x轴交于点E.