Question

12．正六边形ABCDEF的边长为2，则它的面积为6$\sqrt{3}$．

Answer 1

分析 连接OE、OD，由正六边形的特点求出判断出△ODE的形状，作OH⊥ED于H，由特殊角的三角函数值求出OH的长，利用三角形的面积公式即可求出△ODE的面积，进而可得出正六边形ABCDEF的面积．

解答 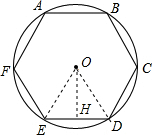解：连接OE、OD，如图所示：
∵六边形ABCDEF是正六边形，
∴∠DEF=120°，
∴∠OED=60°，
∵OE=OD=2，
∴△ODE是等边三角形，
作OH⊥ED于H，则OH=OE•sin∠OED=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，
∴S_△ODE=$\frac{1}{2}$DE•OH=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$，
∴S_{正六边形ABCDEF}=6S_△ODE=6$\sqrt{3}$．
故答案为6$\sqrt{3}$．

点评 本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质；根据题意作出辅助线，构造出等边三角形是解答此题的关键．