题目内容
10.已知a、b是方程x2-3x+m-1=0(m≠1)的两根,在直角坐标系下有A(a,0)、B(0,b),以AB为直径作⊙M,则⊙M的半径的最小值为$\frac{3\sqrt{2}}{4}$.分析 根据根与系数的关系可得a+b=3,由勾股定理可得出AB=$\sqrt{{a}^{2}+{b}^{2}}$,根据完全平方公式可得出AB=$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b),代入a+b的值即可得出AB的最小值,再结合半径与直径的关系即可得出结论.
解答 解:∵a、b是方程x2-3x+m-1=0(m≠1)的两根,
∴a+b=3.
∵A(a,0)、B(0,b),
∴AB=$\sqrt{{a}^{2}+{b}^{2}}$.
∵(a+b)2=a2+b2-2ab≥0,
∴$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b),当a=b时,取等号.
∴⊙M的半径的最小值为$\frac{1}{2}$AB=$\frac{3\sqrt{2}}{4}$.
故答案为:$\frac{3\sqrt{2}}{4}$.
点评 本题考查了根与系数的关系、勾股定理以及两点间的距离公式,利用完全平方公式找出AB=$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b)是解题的关键.

练习册系列答案
相关题目
19.某省为了实现2015年全省森林覆盖率达到63%的目标,大力开展植树造林,已知2013年全省森林覆盖率为60.05%,设从2013年起该省森林覆盖率的年平均增长率为x,则可列方程为( )
| A. | 60.05(1+2x)=63% | B. | 60.05(1+2x)=63 | C. | 60.05(1+x)2=63% | D. | 60.05(1+x)2=63 |
5.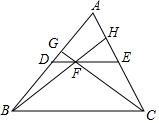 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
 如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )
如图,DE是△ABC的中位线,F为DE上一点,且EF=2DF,BF的延长线交AC于点H,CF的延长线交AB于点G,则S四边形AGFH:S△BFC=( )| A. | 1:10 | B. | 1:5 | C. | 3:10 | D. | 2:5 |
20. 如图,△ACB≌△A′C′B′,∠B=50°,则∠B′的度数为( )
如图,△ACB≌△A′C′B′,∠B=50°,则∠B′的度数为( )
 如图,△ACB≌△A′C′B′,∠B=50°,则∠B′的度数为( )
如图,△ACB≌△A′C′B′,∠B=50°,则∠B′的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 50° |