题目内容
 在平面直角坐标系中,点A(0,2),B(6,4).
在平面直角坐标系中,点A(0,2),B(6,4).(1)请你在x轴上找一点C,使它到点A、B的距离之和为最小,则点C的坐标为
(2)在图中,作出△ABC关于直线x=1的对称图形△A′B′C′;
(3)直接写出△A′B′C′三个顶点坐标.
考点:作图-轴对称变换,轴对称-最短路线问题
专题:
分析:(1)作点A关于x轴的对称点E,连接BE交x轴于点C,利用待定系数法求出直线BE的解析式,令y=0求出x的值即可得出C点坐标;
(2)根据关于直线对称的点的坐标特点画出△ABC关于直线x=1的对称图形△A′B′C′即可;
(3)根据各点在坐标系中的位置写出△A′B′C′三个顶点坐标即可.
(2)根据关于直线对称的点的坐标特点画出△ABC关于直线x=1的对称图形△A′B′C′即可;
(3)根据各点在坐标系中的位置写出△A′B′C′三个顶点坐标即可.
解答: 解:(1)作点A关于x轴的对称点E,连接BE交x轴于点C,则点C即为所求点.
解:(1)作点A关于x轴的对称点E,连接BE交x轴于点C,则点C即为所求点.
设直线BE的解析式为y=kx+b(k≠0),
∵E(0,-2),B(6,4),
∴
,解得
,
∴直线BE的解析式为y=x-2,
∴C(2,0).
故答案为(2,0);
(2)如图所示,△A′B′C′即为所求;
(3)由图可知,A′(2,2),B′(-4,4),C′(0,0).
 解:(1)作点A关于x轴的对称点E,连接BE交x轴于点C,则点C即为所求点.
解:(1)作点A关于x轴的对称点E,连接BE交x轴于点C,则点C即为所求点.设直线BE的解析式为y=kx+b(k≠0),
∵E(0,-2),B(6,4),
∴
|
|
∴直线BE的解析式为y=x-2,
∴C(2,0).
故答案为(2,0);
(2)如图所示,△A′B′C′即为所求;
(3)由图可知,A′(2,2),B′(-4,4),C′(0,0).
点评:本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中正确的是( )
| A、在有理数中,零的意义仅表示没有 |
| B、一个数不是负数就是正数 |
| C、正有理数和负有理数组成全体有理数 |
| D、零是整数 |
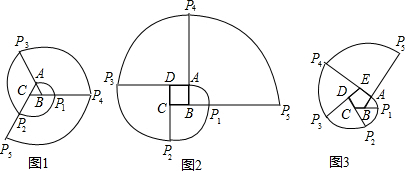
 如图,在⊙O中,
如图,在⊙O中,
 如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,2),C(n,-3),A(2,0),则AD•BC=
如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,2),C(n,-3),A(2,0),则AD•BC=
 如图,⊙O是正三角形ABC的外接圆,点P在劣弧AB上,∠ABP=23°,则∠BCP=
如图,⊙O是正三角形ABC的外接圆,点P在劣弧AB上,∠ABP=23°,则∠BCP=