题目内容
15.方程组$\left\{\begin{array}{l}{\frac{4}{x}+\frac{1}{y}=9}\\{\frac{6}{x}-\frac{2}{y}=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{1}{3}}\end{array}\right.$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:设$\frac{1}{x}$=a,$\frac{1}{y}$=b,方程组课化为得:$\left\{\begin{array}{l}{4a+b=9①}\\{6a-2b=3②}\end{array}\right.$,
①×2+②得:14a=21,即a=$\frac{3}{2}$,
把a=$\frac{3}{2}$代入①得:b=3,
∴$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{1}{3}}\end{array}\right.$,
经检验$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{1}{3}}\end{array}\right.$是原方程组的解.
故答案为:$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{1}{3}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,AE⊥BC与E,且EB=EC,?ABCD的周长为7.6cm,△ABC周长为5.8cm.则AB=2cm.
如图,在?ABCD中,AE⊥BC与E,且EB=EC,?ABCD的周长为7.6cm,△ABC周长为5.8cm.则AB=2cm.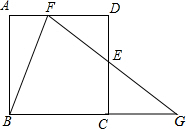 如图,在正方形ABCD中,E是CD的中点,F是AD的一个三等分点,设BC的延长线与FE的延长线相交于G.问BF是否平分∠AFG?请说明理由.
如图,在正方形ABCD中,E是CD的中点,F是AD的一个三等分点,设BC的延长线与FE的延长线相交于G.问BF是否平分∠AFG?请说明理由.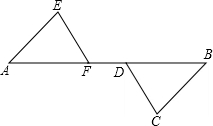 如图,A,F,D,B在同一直线上,AD=BF,AE=BC且AE∥BC.求证:EF∥CD.
如图,A,F,D,B在同一直线上,AD=BF,AE=BC且AE∥BC.求证:EF∥CD. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=30m,EC=15m,CD=30m,则河的宽度AB长为( )
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=30m,EC=15m,CD=30m,则河的宽度AB长为( )