题目内容
3．
如图，在?ABCD中，AE⊥BC与E，且EB=EC，?ABCD的周长为7.6cm，△ABC周长为5.8cm．则AB=2cm．
分析 由平行四边形ABCD的周长为7.6cm，可得AB+BC=3.8cm，又由AE⊥BC于点E，且BE=EC，根据线段垂直平分线的性质，可得AB=AC，继而由△ABC的周长是5.8cm，可得2AB+BC=5.8cm，继而求得答案．
解答 解：∵平行四边形ABCD的周长为7.6cm，
∴AB+BC=3.8cm①，
∵AE⊥BC，且BE=EC，
∴AB=AC，
∵△ABC的周长是5.8cm，
∴2AB+BC=5.8cm②，
②-①得：AB=2cm，
故答案为：2cm．
点评 此题考查了平行四边形的性质、线段垂直平分线的性质以及周长的计算．此题难度不大，熟练掌握平行四边形的性质是解决问题的关键．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
13．若（x+a）（x-b）=x2+mx+n，则m，n的值分别是（ ）
| A． | m=a-b，n=ab | B． | m=-（a-b），n=ab | C． | m=a-b，n=-ab | D． | m=-（a-b），n=-ab |
如图，∠1还可以用∠BCE表示，若∠1=62°9′36″，那么62°9′36″=62.16度．
18．
如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠BAF=60°，则∠DAE=（ ）
如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠BAF=60°，则∠DAE=（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
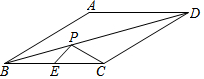已知点E是菱形ABCD边BC上的中点，∠ABC=30°，P是对角线BD上一点，且PC+PE=$\sqrt{26}$．则菱形ABCD面积的最大值是20+8$\sqrt{3}$．
一直角三角形ABC的面积为20，在AB的同侧分别以AB、BC、CA为直径作三个半圆，求阴影部分面积．