题目内容
10．
如图，为估算某河的宽度，在河对岸边选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上．若测得BE=30m，EC=15m，CD=30m，则河的宽度AB长为（ ）| A． | 90m | B． | 60m | C． | 45m | D． | 30m |
分析 求出△ABE和△DCE相似，根据相似三角形对应边成比例列式计算即可得解．
解答 解：∵AB⊥BC，CD⊥BC，
∴∠ABE=∠DCE=90°，
又∵∠AEB=∠DEC（对顶角相等），
∴△ABE∽△DCE，
∴$\frac{AB}{DC}$=$\frac{BE}{CE}$，
即$\frac{AB}{30}$=$\frac{30}{15}$，
解得AB=60m．
故选B．
点评 本题考查了相似三角形的应用，主要利用了相似三角形对应边成比例，确定出相似三角形是解题的关键．
练习册系列答案
口算能手系列答案
相关题目
18．
如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠BAF=60°，则∠DAE=（ ）
如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠BAF=60°，则∠DAE=（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
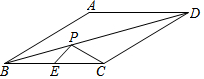已知点E是菱形ABCD边BC上的中点，∠ABC=30°，P是对角线BD上一点，且PC+PE=$\sqrt{26}$．则菱形ABCD面积的最大值是20+8$\sqrt{3}$．