题目内容
5.方程$\frac{3}{2}[{(a-\frac{5}{3})x+\frac{1}{2}}]=1$和方程$\frac{1.7-2x}{0.3}-1=\frac{0.8+x}{0.6}$的解相同,求a的值.分析 先依据解方程的步骤求出方程$\frac{1.7-2x}{0.3}-1=\frac{0.8+x}{0.6}$的解,将x的值代入方程$\frac{3}{2}[{(a-\frac{5}{3})x+\frac{1}{2}}]=1$,求出a的值即可.
解答 解:解方程$\frac{1.7-2x}{0.3}-1=\frac{0.8+x}{0.6}$,
分母化为整数可得:$\frac{17-20x}{3}-1=\frac{8+10x}{6}$,
去分母,得:2(17-20x)-6=8+10x,
去括号,得:34-40x-6=8+10x,
移项、合并同类项,得:-50x=-20,
系数化为1,得:x=$\frac{2}{5}$,
根据题意,将x=$\frac{2}{5}$代入方程$\frac{3}{2}[{(a-\frac{5}{3})x+\frac{1}{2}}]=1$,得:$\frac{3}{2}[\frac{2}{5}(a-\frac{5}{3})+\frac{1}{2}]=1$,
$\frac{3}{5}(a-\frac{5}{3})+\frac{3}{4}=1$,
$\frac{3}{5}a-1+\frac{3}{4}=1$,
$\frac{3}{5}a=\frac{5}{4}$,
a=$\frac{25}{12}$.
点评 本题主要考查解方程的能力,遵循去分母、去括号、移项、合并同类项、系数化为1等基本步骤是基础,观察方程特点简便计算是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列计算正确的是( )
| A. | $\sqrt{(-4)^2}$=-4 | B. | ($\sqrt{2}$)2=4 | C. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | D. | $\sqrt{18}$÷$\sqrt{2}$=3 |
15.计算a2(2a)3-a(3a+8a4)的结果是( )
| A. | 3a2 | B. | -3a | C. | -3a2 | D. | 16a5 |
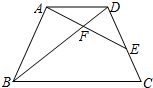 如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD.
如图,在梯形ABCD中,AD∥BC,AB=CD=8,AD=6,E在边CD上,AE与BD相交于点F,∠EAD=∠ABD. 已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.
已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.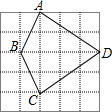 如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.
如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.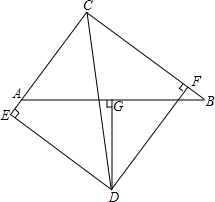 已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.