题目内容
4．
如图，在△ABC中，AD平分∠BAC交BC于D，在AB上截取AE=AC．（1）求证：△ADE≌△ADC；
（2）若AB=6，BC=5，AC=4，求△BDE的周长．
分析 （1）根据SAS证明△ADE≌△ADC即可；
（2）根据全等三角形的性质和线段之间的关系进行解答即可．
解答 证明：（1）∵AD平分∠BAC，
∴∠EAD=∠CDA，
在△ADE与△ADC中，
$\left\{\begin{array}{l}{AE=AC}\\{∠EAD=∠CDA}\\{AD=AD}\end{array}\right.$，
∴△ADE≌△ADC（SAS），
（2）∵△ADE≌△ADC，
∴ED=DC，
∴△BDE的周长=BE+BD+DE=AB-AE+BC-DC+DC=AB-AC+BC-DC+DC=AB-AC+BC=6-4+5=7
点评 此题考查全等三角形的判定和性质，关键是根据SAS证明△ADE≌△ADC．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
14．如图，△ABC与△A′B′C′关于直线MN对称，P为MN上任意一点，下列说法不正确的是（ ）
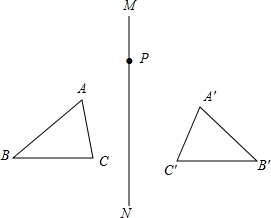
| A． | AP=A′P | B． | MN垂直平分AA′，CC′ | ||
| C． | 这两个三角形的面积相等 | D． | 直线AB、A′B的交点不一定在MN上 |
15．聪明好学的王明用计算机自己设计了一个计算程序，输入和输出的数据如下表：
那么，
（1）当输入数据10时，输出的数据是$\frac{10}{101}$．
（2）当输入数据n时，输出的数据是$\frac{n}{{n}^{2}+1}$（用n的代数式表示）．
| 输入 | … | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 输出 | … | $\frac{1}{2}$ | $\frac{2}{5}$ | $\frac{3}{10}$ | $\frac{4}{17}$ | $\frac{5}{26}$ | $\frac{6}{37}$ | … |
（1）当输入数据10时，输出的数据是$\frac{10}{101}$．
（2）当输入数据n时，输出的数据是$\frac{n}{{n}^{2}+1}$（用n的代数式表示）．
细图，已知∠MON=90°，在它的两边上截取OA=OB，并在它的内部任作一射线OP，作AD⊥OP于D，BE⊥OP于E．
8．
如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$，那么点B′的坐标是（ ）
如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$，那么点B′的坐标是（ ）| A． | （3，2） | B． | （-2，-3） | C． | （2，3）或（-2，-3） | D． | （3，2）或（-3，-2） |
如图，把一张长方形纸片ABCD沿对角线BD折叠，使C点落在C′，且BC′与AD交于E点．