题目内容
5. 如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点.
如图,把一张长方形纸片ABCD沿对角线BD折叠,使C点落在C′,且BC′与AD交于E点.(1)试判断重叠部分三角形BED的形状,并证明你的结论;
(2)若BE平分∠ABD,AB=3,求BD的长.
分析 (1)根据折叠的性质可得,∠C=∠C'=90°,∠BDC'=∠BDC,然后根据矩形的性质,可得∠ABD=∠CDB,由∠ABD+∠ADB=∠C'DB+∠C'BD=90°,得出∠ADB=∠C'BD,证得△BED为等腰三角形;
(2)由角平分线的性质可得∠ABE=∠EBD,求出∠ABE=∠EBD=30°,在直角△ABD中,求出BD的长度.
解答 解:(1)由折叠的性质可得,∠C=∠C'=90°,∠BDC'=∠BDC,
在矩形ABCD中,
∵AB∥CD,
∴∠ABD=∠CDB,
∴∠BDC'=∠CDB,
∵∠A=∠C=∠C'=90°,
∴∠ABD+∠ADB=∠C'DB+∠C'BD=90°,
∴∠ADB=∠C'BD,
∴△BED为等腰三角形;
(2)∵BE平分∠ABD,
∴∠ABE=∠EBD,
∵∠EBD=∠DBC,
∴∠ABE=∠EBD=∠EBD=30°,
在Rt△ABD中,
∵AB=3,
∴BD=2AB=6..
点评 本题考查了折叠的性质,涉及了矩形的性质、角平分线的性质,注意掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
20.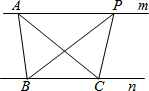 如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
 如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )
如图,A、P是直线m上的任意两个点,B、C是直线n上的两个定点,且直线m∥n;则下列说法正确的是( )| A. | AB∥PC | B. | △ABC的面积等于△BCP的面积 | ||
| C. | AC=BP | D. | △ABC的周长等于△BCP的周长 |
14.当三角形的面积S一定时,它的高h与底边a之间的关系是( )
| A. | 正比例函数关系 | B. | 反比例函数关系 | C. | 一次函数关系 | D. | 不是函数关系 |
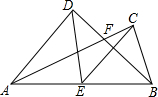 如图.已知AD⊥BD,AC⊥BC,AC与BD交于点F,E为AB的中点,
如图.已知AD⊥BD,AC⊥BC,AC与BD交于点F,E为AB的中点, 如图,在△ABC中,AD平分∠BAC交BC于D,在AB上截取AE=AC.
如图,在△ABC中,AD平分∠BAC交BC于D,在AB上截取AE=AC.