题目内容
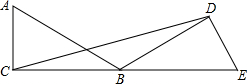 如图,把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.(1)三角板旋转来多少度?
(2)连结CD,求∠BDC的度数;
(3)若AC=4,求△CBD的面积.
考点:旋转的性质
专题:
分析:(1)三角尺旋转的角度即为∠ABE的度数,而∠ABE和三角尺的30°角互为补角,由此可求出旋转的度数;
(2)由旋转的性质知:BC=BD,由此可得出△BCD的形状,进而求出∠BDC的度数;
(3)首先求出BC,DF的长,再利用三角形面积公式求出即可.
(2)由旋转的性质知:BC=BD,由此可得出△BCD的形状,进而求出∠BDC的度数;
(3)首先求出BC,DF的长,再利用三角形面积公式求出即可.
解答:解:(1)∵把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,
∴∠ABC=30°,
∴∠DBE=30°,
∴∠ABE=180°-30°=150°,即旋转了150°;
(2)根据旋转的性质知,CB=BD,故△CBD为等腰三角形,
故∠BDC=∠BCD=
=15°;
 (3)过点D作DF⊥BE于点F,
(3)过点D作DF⊥BE于点F,
∵∠ABC=30°,AC=4,
∴BC=
=4
,BE=8,
∵DF×BE=BD×DE,
∴8DF=4
×4,
解得:DF=2
,
故△CBD的面积为:
×BC×DF=
×4
×2
=12.
∴∠ABC=30°,
∴∠DBE=30°,
∴∠ABE=180°-30°=150°,即旋转了150°;
(2)根据旋转的性质知,CB=BD,故△CBD为等腰三角形,
故∠BDC=∠BCD=
| 180°-150° |
| 2 |
 (3)过点D作DF⊥BE于点F,
(3)过点D作DF⊥BE于点F,∵∠ABC=30°,AC=4,
∴BC=
| 4 |
| tan30° |
| 3 |
∵DF×BE=BD×DE,
∴8DF=4
| 3 |
解得:DF=2
| 3 |
故△CBD的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题主要考查了直角三角形的性质、旋转的性质、三角形面积的计算方法等知识点,得出DF的长是解题关键.

练习册系列答案
相关题目
下列说法正确的是( )
①0是整数;②-2是负分数;③3.5不是整数;④自然数一定是正数.
①0是整数;②-2是负分数;③3.5不是整数;④自然数一定是正数.
| A、1个 | B、2个 | C、3个 | D、4个 |
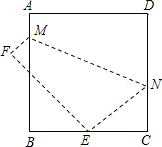 如图,将边长为4cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN交AB于M,交DC于N,则线段FM长为
如图,将边长为4cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN交AB于M,交DC于N,则线段FM长为