题目内容
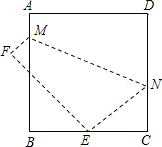 如图,将边长为4cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN交AB于M,交DC于N,则线段FM长为
如图,将边长为4cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN交AB于M,交DC于N,则线段FM长为考点:翻折变换(折叠问题)
专题:
分析:根据线段中点的定义可得CE=
BC=2,再根据翻折变换的性质可得EN=DN,设CN=x,表示出EN,然后利用勾股定理列方程求出x,过点M作MG⊥CD于G,连接DE,根据翻折的性质可得MN⊥DE,再求出∠NMG=∠EDC,然后利用“角边角”证明△CDE和△GMN全等,根据全等三角形对应边相等可得GN=CE,然后求出DG,再求出AM=DG,然后根据翻折的性质可得FM=AM.
| 1 |
| 2 |
解答: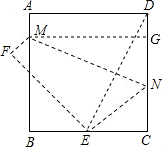 解:∵点E为BC的中点,
解:∵点E为BC的中点,
∴CE=
BC=2,
由翻折的性质得,EN=DN,
设CN=x,则EN=DN=4-x,
在Rt△CEN中,CE2+CN2=EN2,
即22+x2=(4-x)2,
解得x=
,
过点M作MG⊥CD于G,连接DE,则MG=CD,
由翻折的性质得,MN⊥DE,
∴∠NMG=∠EDC,
在△CDE和△GMN中,
,
∴△CDE≌△GMN(ASA),
∴GN=CE=2cm,
∴DG=4-
-2=
cm,
∵MG⊥CD,四边形ABCD是正方形,
∴四边形AMGD是矩形,
∴AM=DG,
由翻折的性质得,FM=AM=
cm.
故答案为:
cm.
 解:∵点E为BC的中点,
解:∵点E为BC的中点,∴CE=
| 1 |
| 2 |
由翻折的性质得,EN=DN,
设CN=x,则EN=DN=4-x,
在Rt△CEN中,CE2+CN2=EN2,
即22+x2=(4-x)2,
解得x=
| 3 |
| 2 |
过点M作MG⊥CD于G,连接DE,则MG=CD,
由翻折的性质得,MN⊥DE,
∴∠NMG=∠EDC,
在△CDE和△GMN中,
|
∴△CDE≌△GMN(ASA),
∴GN=CE=2cm,
∴DG=4-
| 3 |
| 2 |
| 1 |
| 2 |
∵MG⊥CD,四边形ABCD是正方形,
∴四边形AMGD是矩形,
∴AM=DG,
由翻折的性质得,FM=AM=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了翻折变换的性质,全等三角形的性质,正方形的性质,勾股定理,熟记性质并作辅助线构造出全等三角形是解题的关键,难点在于利用勾股定理列出方程.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
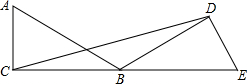 如图,把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
如图,把一块直角三角板ABC绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.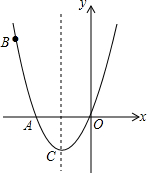 如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过A(-2,0),B(-3,3)及原点O,顶点为C. 如图,过圆周上一点P作直径AB的垂线PM,M为垂足,过P及A作圆的切线交于Q,BQ交PM于N,求证:PN=MN.
如图,过圆周上一点P作直径AB的垂线PM,M为垂足,过P及A作圆的切线交于Q,BQ交PM于N,求证:PN=MN.