题目内容
14. 在平面直角坐标系xOy中,己知A(-1,5),B(4,2),C(-1,0)三点.
在平面直角坐标系xOy中,己知A(-1,5),B(4,2),C(-1,0)三点.(1)点A关于原点O的对称点A′的坐标为(1,-5),点B关于x轴的对称点B′的坐标为(4,-2),点C关于y轴的对称点C′的坐标为(1,0).
(2)在图中画出△A′B′C′,并求它的面积.
分析 (1)l根据点关于原点对称、关于x轴的对称和关于y轴对称的点的坐标特征求解;
(2)利用三角形面积公式求解.
解答 解:(1)点A关于原点O的对称点A′的坐标为 (1,-5),点B关于x轴的对称点B′的坐标为(-4,-2),点C关于y轴的对称点C′的坐标为(1,0).
(2)△A′B′C′的面积=$\frac{1}{2}$×5×3=$\frac{15}{2}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
2.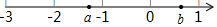 若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )
若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )
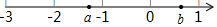 若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )
若有理数a、b在数轴上的位置如图所示,下列说法不正确的是( )| A. | |a|>|b| | B. | -2<a<-1,0<b<1 | C. | a+b<0 | D. | a>-1,0<b<1 |
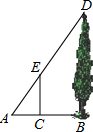 如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为1.8m,并测得AC=0.9m,AB=2.1m,那么大树DB的高度是4.2m.
如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为1.8m,并测得AC=0.9m,AB=2.1m,那么大树DB的高度是4.2m.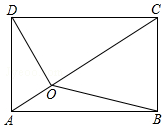 如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为2$\sqrt{2}$.
如图,已知O是矩形ABCD内一点,且OA=1,OB=3,OC=4,那么OD的长为2$\sqrt{2}$.