题目内容
2.关于二次函数y=ax2+bx+c(a≠0)的图象有下列命题,其中错误的是( )| A. | 当c=0时,函数的图象经过原点 | |
| B. | 当b=0时,函数的图象关于y轴对称 | |
| C. | 若函数的图象过点A(1,2),B(7,2),则它的对称轴为直线x=3 | |
| D. | 当c>0且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根 |
分析 利用二次函数的性质,根据二次函数解析式的系数与图象的关系,逐一分析判断即可.
解答 解:A、二次函数y=ax2+bx+c中令x=0代入得到y=c=0,即函数经过原点,正确;
B、当b=0时,函数是y=ax2+c,函数的图象关于y轴对称,正确;
C、若函数的图象过点A(1,2),B(7,2),则它的对称轴为直线x=4,错误;
D、图象的开口向下,则a<0,又c>0,△=b2-4ac>0,方程必有两个不相等的实根,正确.
故选:C.
点评 此题考查二次函数的性质,掌握二次函数中a,b,c符号的确定方法以及与图象的关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知a和b一正一负,则$\frac{|a|}{a}$+$\frac{|b|}{b}$的值为( )
| A. | 0 | B. | 2 | C. | -2 | D. | 根据a、b的值确定 |
11.“十一”节期间,某商品按成本价提高30%后标价,再打8折(标价的80%)销售,售价为240元.设该商品的成本价为x元,根据题意,下面所列方程正确的是( )
| A. | x•30%•80%=240 | B. | x•(1+30%)•80%=240 | ||
| C. | x•(1+30%)•(1-80%)=240 | D. | x•30%=240•80% |
 如图,点A、B、C在⊙O上,D是$\widehat{AB}$的中点,CD交OB于点E,若∠AOB=100°,∠OBC=55°,求∠OEC的度数.
如图,点A、B、C在⊙O上,D是$\widehat{AB}$的中点,CD交OB于点E,若∠AOB=100°,∠OBC=55°,求∠OEC的度数.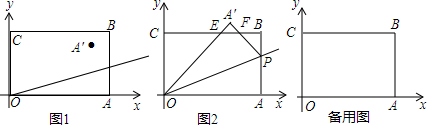
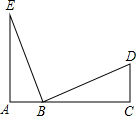 如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件AE=CB,使得△EAB≌△BCD,理由是SAS.
如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件AE=CB,使得△EAB≌△BCD,理由是SAS.