题目内容
14．若（x+2）2+|y+3|=0，则yz的值是$\frac{1}{9}$．分析 直接利用偶次方的性质以及绝对值的性质得出x，y的值，进而利用负整数指数幂的性质求出即可．
解答 解：∵（x+2）2+|y+3|=0，
∴x+2=0，y+3=0，
解得：x=-2，y=-3，
故yz=（-3）-2=$\frac{1}{（-3）^{2}}$=$\frac{1}{9}$．
故答案为：$\frac{1}{9}$．
点评 此题主要考查了偶次方的性质以及绝对值的性质，正确得出x，y的值是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．关于二次函数y=ax2+bx+c（a≠0）的图象有下列命题，其中错误的是（ ）
| A． | 当c=0时，函数的图象经过原点 | |
| B． | 当b=0时，函数的图象关于y轴对称 | |
| C． | 若函数的图象过点A（1，2），B（7，2），则它的对称轴为直线x=3 | |
| D． | 当c＞0且函数的图象开口向下时，方程ax2+bx+c=0必有两个不相等的实根 |
19．如果点M（a，a+1）在x轴上，则a的值为（ ）
| A． | a=1 | B． | a=-1 | C． | a＞0 | D． | a的值不能确定 |
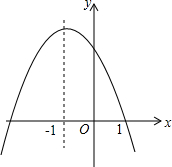二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，给出以下结论：①a+b+c＜0；②c-a＞0；③a-2b+4c＞0；④m（am+b）+b＜a（m≠-1），其中正确的结论的个数是（ ）