题目内容
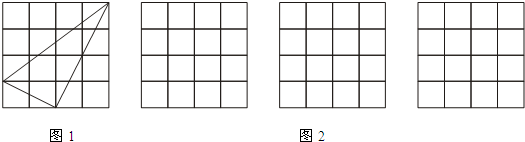
5.按下列要求作图:(1)在正方形网格中三条不同实线上各取一个格点,使其中任意两点,不在同一实线上.
(2)连结三个格点,使之构成直角三角形(如图1),请在图2网格中作出三个直角三角形,使四个直角三角形互不全等.
分析 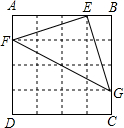 本题中得出直角三角形的方法如图:如果设AE=x,BE=4-x,如果∠FEG=90°,△AFE∽△GBE,则有AF•BG=AE•BE=x(4-x),当x=1时,AF•BG=3,AF=1,BG=3或AF=3,BG=1;当x=2时,AF•BG=4,AF=1,BG=4或AF=2,BG=2或AF=4,BG=1;当x=3时,AF•BG=3,AF=1,BG=3或AF=3,BG=1(同x=1时).由此可画出另两种图形.
本题中得出直角三角形的方法如图:如果设AE=x,BE=4-x,如果∠FEG=90°,△AFE∽△GBE,则有AF•BG=AE•BE=x(4-x),当x=1时,AF•BG=3,AF=1,BG=3或AF=3,BG=1;当x=2时,AF•BG=4,AF=1,BG=4或AF=2,BG=2或AF=4,BG=1;当x=3时,AF•BG=3,AF=1,BG=3或AF=3,BG=1(同x=1时).由此可画出另两种图形.
解答 解:如图2所示,网格中作出三个直角三角形,使四个直角三角形互不全等.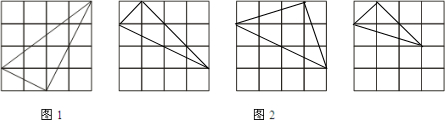
点评 本题考查了勾股定理,利用了勾股定理、相似三角形的判定和性质等知识来得出有可能的直角三角形的情况,要学会对已学知识点的运用.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
12.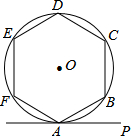 如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
 如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )
如图,正六边形ABCDEF内接于⊙O,若直线PA与⊙O相切于点A,则∠PAB=( )| A. | 30° | B. | 35° | C. | 45° | D. | 60° |
13.我州今年参加中考的学生人数大约为5.08×104人,对于这个用科学记数法表示的近似数,下列说法正确的是( )
| A. | 精确到百分位,有3个有效数字 | B. | 精确到百分位,有5个有效数字 | ||
| C. | 精确到百位,有3个有效数字 | D. | 精确到百位,有5个有效数字 |
20.方程x(x+1)=5(x+1)的根是( )
| A. | -1 | B. | 5 | C. | 1 或5 | D. | -1或5 |
10.下列变形中,属因式分解的是( )
| A. | 2x-2y=2(x-y) | B. | (x+y)2=x2+2xy+y2 | C. | (x+2y)(x-2y)=x2-2y2 | D. | x2-4x+5=(x-2)2+1 |