题目内容
3.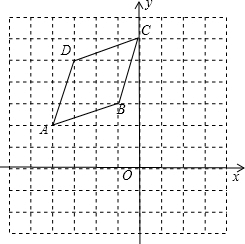 如图,平面直角坐标系中,菱形ABCD的四个顶点都在正方形网格的格点上.
如图,平面直角坐标系中,菱形ABCD的四个顶点都在正方形网格的格点上.(1)画出菱形ABCD绕点A顺时针旋转90°后得到的菱形AB1C1D1;
(2)填空:菱形ABCD与菱形AB1C1D1成轴对称.并在图中画出对称轴l或对称中心P;
(3)直接写出菱形ABCD在旋转过程中所扫过的面积.
分析 (1)利用旋转的性质得出对应点位置进而得出答案;
(2)利用轴对称图形的性质得出对称轴即可;
(3)利用旋转的性质结合扇形面积求法得出答案.
解答 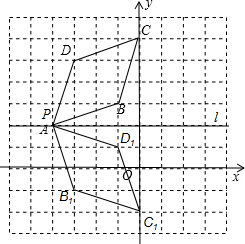 解:(1)如图所示:菱形AB1C1D1,即为所求;
解:(1)如图所示:菱形AB1C1D1,即为所求;
(2)如图所示:菱形ABCD与菱形AB1C1D1成轴对称,对称轴为直线l;
故答案为:轴;
(3)菱形ABCD在旋转过程中所扫过的面积为:$\frac{1}{2}$×$\sqrt{2}$×4$\sqrt{2}$+$\frac{90π×(4\sqrt{2})^{2}}{360}$=4+8π.
点评 此题主要考查了旋转变换和轴对称图形的性质和扇形面积求法,根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
17.下列哪个点一定在双曲线y=$\frac{6}{x}$的图象上( )
| A. | (1,5) | B. | (-1,6) | C. | (-1,-6) | D. | (2,-3) |
18.使函数y=$\sqrt{x-2}$有意义的x的取值范围是( )
| A. | x<2 | B. | x>2 | C. | x≤2 | D. | x≥2 |
8.一个物体向西移动5米记作-5米,这个物体又移动了若干米,停留在两次移动前的位置的西边1米处.能反映这个物体第二次移动的方向和路程的算式是( )
| A. | -1-(-5) | B. | 1+(-5) | C. | -1+(-5) | D. | 1-(-5) |
