题目内容
15. 如图,在由六个全等的正三角形拼成的图中,菱形的个数为( )
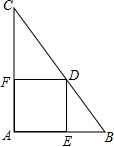
如图,在由六个全等的正三角形拼成的图中,菱形的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据等边三角形的性质,易判定EF∥AD∥BC,ED∥FC∥AB,CD∥BE∥AF,然后根据平行四边形的判定再由等边三角形的性质即可求解得出结论;
解答 解:如图,
由题意可知,EF∥AD∥BC,ED∥FC∥AB,CD∥BE∥AF,有ED=EF=AF=AB=BC=CD=GE=GF=GA=GB=GC=GD,
∴四边形EDGF,EDCG,FGBA,GCBA,EGAF,CDGB是平行四边形,
∵AB=BC=CD=DE=EF=AF,
∴平行四边形EDGF,EDCG,FGBA,GCBA,EGAF,CDGB都是菱形,共6个.
故选D.
点评 本题是菱形的判定,结合等边三角形的性质考查了菱形的判定,在应用判定定理判定菱形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.

练习册系列答案
相关题目
5.设甲数为m,若甲数是乙数的2倍,则乙数用单项式表示是( )
| A. | 2m | B. | $\frac{1}{2}$m | C. | 3m | D. | $\frac{1}{3}$m |
6. 如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
 如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{24}{5}$ | C. | 5 | D. | $\frac{11}{2}$ |
10.若实数x,y满足(x2+y2)2+2(x2+y2)=0,则x2+y2的值为( )
| A. | 0 | B. | -2 | C. | 0或-2 | D. | 0或2 |
20.下列直线是圆的切线的是( )
| A. | 与圆有公共点的直线 | B. | 到圆心的距离等于半径的直线 | ||
| C. | 到圆心的距离大于半径的直线 | D. | 到圆心的距离小于半径的直线 |
7.下列方程中,以x=1为解的方程是( )
| A. | 3-(x-1)=4 | B. | 5x-2=x-4 | C. | 2x-1=5 | D. | 2x-1=4-3x |
 如图,∠A是⊙O的圆周角,∠A=40°,则∠OBC的度数为50°.
如图,∠A是⊙O的圆周角,∠A=40°,则∠OBC的度数为50°.