题目内容
18.下列等式或说法一定正确的是( )| A. | $\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$ | B. | $\sqrt{{a}^{2}-{b}^{2}}$不是最简根式 | ||
| C. | 若a<0,则$\sqrt{{a}^{4}}$=a2 | D. | $\sqrt{18}$或$\sqrt{48}$是同类二次根式 |
分析 结合同类二次根式、最简二次根式和二次根式的乘除法的概念进行判断求解即可.
解答 解:A、当a≥0,b>0时,$\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$才成立,故本选项错误;
B、$\sqrt{{a}^{2}{-b}^{2}}$是最简根式,本选项错误;
C、当a<0,则$\sqrt{{a}^{4}}$=a2,本选项正确;
D、$\sqrt{18}$=3$\sqrt{2}$,$\sqrt{48}$=4$\sqrt{3}$,故$\sqrt{18}$和$\sqrt{48}$不是同类二次根式,本选项错误.
故选C.
点评 本题考查了同类二次根式、最简二次根式和二次根式乘除法的知识,解答本题的关键在于熟练掌握各知识点的概念.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.Rt△ABC中,∠C=90°,AC=5,BC=12,则连接两条直角边中点的线段长为( )
| A. | 13 | B. | 6.5 | C. | 7 | D. | 8 |
6.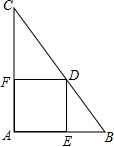 如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
 如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{24}{5}$ | C. | 5 | D. | $\frac{11}{2}$ |
10.若实数x,y满足(x2+y2)2+2(x2+y2)=0,则x2+y2的值为( )
| A. | 0 | B. | -2 | C. | 0或-2 | D. | 0或2 |
7.下列方程中,以x=1为解的方程是( )
| A. | 3-(x-1)=4 | B. | 5x-2=x-4 | C. | 2x-1=5 | D. | 2x-1=4-3x |