题目内容
6.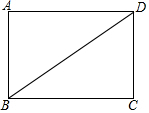 矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积.
矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积.
分析 利用矩形的性质可知CD=AB,在Rt△BCD中可求得BD,利用矩形的面积公式可求得其面积.
解答 解:
∵四边形ABCD为矩形,
∴CD=AB=2$\sqrt{3}$厘米,
在Rt△BCD中,由勾股定理可得BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{3})^{2}}$=4$\sqrt{3}$(厘米),
S矩形ABCD=AB•BC=2$\sqrt{3}$×6=12$\sqrt{3}$(平方厘米),
即矩形ABCD的对角线BD的长为4$\sqrt{3}$厘米,面积为12$\sqrt{3}$平方厘米.
点评 本题主要考查矩形的性质,掌握矩形的每个角都是直角,利用勾股定理是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
16.某校学生会为了了解本校2000名学生的上学方式,采用问卷的方式对一部分学生进行了调查,在确定调查对象时,大家提出了两种方案:(A)在全校随机抽取150名学生进行调查.(B)在七年级随机抽取150名学生进行调查,学生会选择了其中的一种正确的调查方案,在问卷调查时,每位被调查时,每位被调查的学生都选择了问卷中的一种上学方式,学生会将收集到的数据进行整理,绘制成如下的统计表.
某校150名学生上学方式统计表
(1)学生会在确定调查对象时选择的正确方案是A(填“A”或“B”).
(2)根据抽样调查的结果,将估计出的全校2000名上学方式的情况绘制成合适的统计图(绘制一种即可)
(3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议,如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化建议.
某校150名学生上学方式统计表
| 方式 | 划记 | 频数 |
| 步行 | 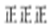 | 15 |
| 骑车 | 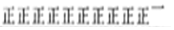 | 51 |
| 乘公共交通工具 | 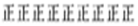 | 45 |
| 乘私家车 |  | 30 |
| 其他 |  | 9 |
| 合计 | 150 |
(2)根据抽样调查的结果,将估计出的全校2000名上学方式的情况绘制成合适的统计图(绘制一种即可)
(3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议,如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地,请你结合上述统计的全过程,再提出一条合理化建议.
16.下列图形既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )度.
如图,已知∠A=70°,O是AB上一点,直线OD与AB的夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )度.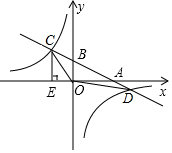 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别与x轴、y轴交于点B和A,与反比例函数y=-$\frac{24}{x}$的图象交于C、D两点,且C点坐标为(-4,m),D点坐标为(12,-2),CE⊥x轴于点E.