题目内容
11.简便计算(1)$\frac{1999199{8}^{2}}{1999199{7}^{2}+1999199{9}^{2}-2}$
(2)(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{9{9}^{2}}$)
分析 (1)设a=19991998,表示出19991997与19991999,计算即可得到结果;
(2)原式利用平方差公式变形,计算即可得到结果.
解答 解:(1)设a=19991998,则19991997=a-1,19991999=a+1,
原式=$\frac{{a}^{2}}{(a-1)^{2}+(a+1)^{2}-2}$=$\frac{{a}^{2}}{2{a}^{2}}$=$\frac{1}{2}$;
(2)原式=(1+$\frac{1}{2}$)(1-$\frac{1}{2}$)(1+$\frac{1}{3}$)(1-$\frac{1}{3}$)…(1+$\frac{1}{99}$)(1-$\frac{1}{99}$)
=$\frac{3}{2}$×$\frac{4}{3}$×…×$\frac{100}{99}$×$\frac{1}{2}$×$\frac{2}{3}$×…×$\frac{98}{99}$
=50×$\frac{1}{99}$
=$\frac{50}{99}$.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
19.下列各式的计算中,正确的是( )
| A. | $\sqrt{(-16)×(-25)}$=$\sqrt{(-16)}$×$\sqrt{(-25)}$=20 | B. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | ||
| C. | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{81×1}$=9 | D. | 3$\sqrt{\frac{2}{3}}$=$\sqrt{2}$ |
16.下列方程中,无理方程是( )
| A. | $\sqrt{2}$x2-1=0 | B. | 1-$\frac{\sqrt{2}}{x}$=0 | C. | $\sqrt{2x}$-1=0 | D. | 1-$\sqrt{2}x$=0 |
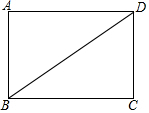 矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积.
矩形ABCD的两边分别为AB=2$\sqrt{3}$厘米,BC=6厘米,求对角线BD的长和矩形ABCD的面积. 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.