题目内容
16.定义一种运算“⊕”如下:$\left\{\begin{array}{l}{a⊕b=a+b(a>b)}\\{a⊕b=b-a(a≤b)}\end{array}\right.$,若(2x-3)⊕(x+1)=1,则( )| A. | x=1 | B. | x=3 | C. | x=-3 | D. | x=1或x=3 |
分析 利用题中的新定义化简已知等式,求出x的值即可.
解答 解:根题中的新定义得:当2x-3>x+1,即x>4时,(2x-3)⊕(x+1)=2x-3+x+1=1,
解得:x=1,不合题意,舍去;
当2x-3≤1+x,即x≤4时,(2x-3)⊕(x+1)=x+1-2x+3=1,
解得:x=3,
故选B
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
7.下列分解因式结果正确的是( )
| A. | a2b+7ab-b=b(a2+7a) | B. | 3x2y-3xy+6y=3y(x2-x-2) | ||
| C. | 8xyz-6x2y2=2xyz(4-3xy) | D. | -2a2+4ab-6ac=-2a(a-2b+3c) |
1.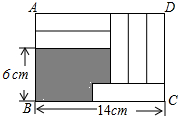 在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
 在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )
在长方形ABCD中,放入6个形状、大小相同的长方形,所标尺寸如图所示,则阴影部分的面积为( )| A. | 38cm2 | B. | 42cm2 | C. | 40cm2 | D. | 44cm2 |
8.-3的绝对值等于( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 小于3 |
6.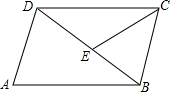 如图,在?ABCD中,AB=BD,点E在BD上,CE=CB.如果∠A=70°,那么∠DCE等于( )
如图,在?ABCD中,AB=BD,点E在BD上,CE=CB.如果∠A=70°,那么∠DCE等于( )
 如图,在?ABCD中,AB=BD,点E在BD上,CE=CB.如果∠A=70°,那么∠DCE等于( )
如图,在?ABCD中,AB=BD,点E在BD上,CE=CB.如果∠A=70°,那么∠DCE等于( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
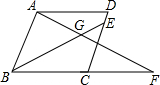 如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?
如图,菱形ABCD,∠ABC=60°,动点E、F分别从C点与B点出发,速度同为1单位/s,AB=4,F点先出发,若AF、BE相交于G,且∠AGB=60°时,问动点F与动点E出发时间有什么关系.此时$\frac{AF}{BE}$为多少?


