题目内容
7.以下四个命题中真命题是( )①三角形有且只有一个内切圆;
②四边形的内角和与外角和相等;
③顺次连接四边形各边中点所得的四边形一定是菱形;
④一组对边平行且一组对角相等的四边形是平行四边形.
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ②③④ |
分析 分别利用三角形内切圆的性质以及多边形内角和定理以及中点四边形的性质和平行四边形的判定方法分析得出答案.
解答 解:①三角形有且只有一个内切圆,正确;
②四边形的内角和与外角和相等,正确;
③顺次连接四边形各边中点所得的四边形一定是平行四边形,故此选项错误;
④一组对边平行且一组对角相等的四边形是平行四边形,正确,
理由:连接BD,
∵AB∥CD,
∴∠ABD=∠CDB,
在△ABD和△CDB中,
$\left\{\begin{array}{l}{BD=DB}\\{∠ABD=∠CDB}\\{AB=CD}\end{array}\right.$,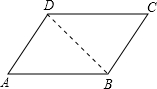
∴△ABD≌△CDB(SAS),
∴∠ADB=∠CBD,
∴AD∥BC.
又AB∥CD,
∴四边形ABCD是平行四边形.
故正确的有:①②④.
故选:C.
点评 此题主要考查了命题与定理,正确把握中点四边形以及平行四边形的判定方法是解题关键.

练习册系列答案
相关题目
17. 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
 如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的大小是( )| A. | 100° | B. | 80° | C. | 60° | D. | 40° |
15.若分式$\frac{{{x^2}-4}}{(x+1)(x-2)}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 2或-1 |
2.小亮所在的校篮球队12名队员的平均身高为1.82米,小亮的身高是1.84米,则下列说法正确的是( )
| A. | 篮球队员身高的中位数一定大于1.82米 | |
| B. | 篮球队员身高的众数一定小于1.82米 | |
| C. | 篮球队中比小亮高的队员不会超过5人 | |
| D. | 篮球队员身高的中位数与众数有可能相同 |
12.在一次体育达标测试中,小明所在小组的六位同学的立定跳远成绩如下(单位:m):2.00,2.11,2.21,2.15,2.20,2.17,那么这组数据的中位数是( )
| A. | 2.16 | B. | 2.15 | C. | 2.14 | D. | 2.13 |
16.使$\sqrt{3x-1}$有意义的x的取值范围是( )
| A. | x>-$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x≥$\frac{1}{3}$ | D. | x≥-$\frac{1}{3}$ |
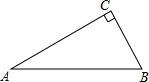 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.