题目内容
9. 如图,∠A0B=60°,点P在0A上,点M、N在OB上,PM=PN,若OP=10,OM=4,则MN的长为( )
如图,∠A0B=60°,点P在0A上,点M、N在OB上,PM=PN,若OP=10,OM=4,则MN的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 作PC⊥OB于点C,根据等腰三角形的性质得到MC=CN,根据直角三角形的性质得到OC=$\frac{1}{2}$OP=5,求出MC的长,得到答案.
解答 解: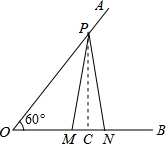 作PC⊥OB于点C,
作PC⊥OB于点C,
∵PM=PN,PC⊥OB,
∴MC=CN,
∵PC⊥OB,∠A0B=60°,
∴∠OPC=30°,
∴OC=$\frac{1}{2}$OP=5,又OM=4,
∴MC=1,
∴MN=2,
故选:B.
点评 本题考查的是直角三角形的性质和等腰三角形的性质,掌握30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
19.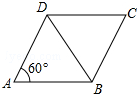 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )
如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )
 如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )
如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
4.8名学生的成绩分别为:80、82、78、80、74、78、x、81,这组成绩的众数是78,则x为( )
| A. | 76 | B. | 78 | C. | 80 | D. | 82 |
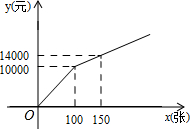 在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案: 已知等腰Rt△ABC,BD是AC边上的中线,∠CBD=∠ACE.求证:∠CDF=∠ADE.
已知等腰Rt△ABC,BD是AC边上的中线,∠CBD=∠ACE.求证:∠CDF=∠ADE.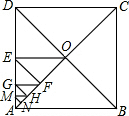 如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )
如图,在正方形ABCD中,AO⊥BD、OE、FG、HM都垂直于AD,EF、GH、MN都垂直于AO,如果△AMN的面积为1,那么正方形ABCD的边长等于( )