Question

20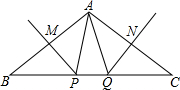．如图，在△ABC中，PM、QN分别是AB、AC的垂直平分线，∠BAC=100°，则∠PAQ等于20°，若BC=10，则△PAQ的周长等于10．

Answer 1

分析 由在△ABC中，PM、QN分别是AB、AC的垂直平分线，根据线段垂直平分线的性质，可求得∠PAB=∠B，∠CAQ=∠C，又由∠BAC=110°，易求得∠PAB+∠CAQ的度数，继而求得∠PAQ的度数，根据线段垂直平分线的性质得到PA=PB，AQ=CQ，等量代换即可得到结论．

解答 解：∵在△ABC中，PM、QN分别是AB、AC的垂直平分线，
∴PA=PB，AQ=CQ，
∴∠PAB=∠B，∠CAQ=∠C，
∵∠BAC=100°，
∴∠B+∠C=180°-∠BAC=80°，
∴∠PAB=∠CAQ=80°，
∴∠PAQ=∠BAC-（∠PAB+∠CAQ）=100°-80°=20°，
∵PA=PB，AQ=CQ，
∴△PAQ的周长=PA+PQ+AQ=PB+PQ+CQ=BC=10，
故答案为：20°，10．

点评 此题考查了线段垂直平分线的性质以及三角形内角和定理．此题难度不大，熟练掌握线段垂直平分线的性质是解题的关键．