题目内容
15. 如图,在△ABC中,AB=AC=BC=6,求△ABC外接圆⊙O的半径r.
如图,在△ABC中,AB=AC=BC=6,求△ABC外接圆⊙O的半径r.
分析 作直径AD,连接BD,根据等边三角形性质求出∠C=60°,根据圆周角定理求出∠D=∠C=60°,解直角三角形求出AD,即可得出结果.
解答 解:如图,作直径AD,连接BD,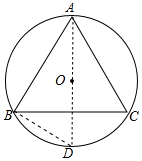
∵等边△ABC内接于⊙O,AD为直径,
∴∠D=∠C=60°,∠ABD=90°,
∴AD=$\frac{AB}{sin60°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$=4$\sqrt{3}$,
∴△ABC外接圆⊙O的半径r=$\frac{1}{2}$AD=2$\sqrt{3}$.
点评 本题考查的是三角形的外接圆与外心,涉及到等边三角形的性质,圆周角定理,解直角三角形的应用,关键是能正确作出辅助线.

练习册系列答案
相关题目
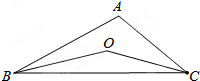 如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°.
如图,BO、CO分别平分∠ABC、∠ACB,∠A=100°,则∠BOC的度数为140°.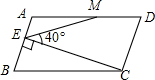 如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°.
如图,在平行四边形ABCD中,AD=2AB,M是AD的中点,CE⊥AB于点E,∠CEM=40°,则∠AME的度数是30°. 如图,△ABC∽△DBE,点E在AC上,∠ABC=∠DBE=90°,连接AD,求证:AD⊥AC.
如图,△ABC∽△DBE,点E在AC上,∠ABC=∠DBE=90°,连接AD,求证:AD⊥AC.