题目内容
20.(1)$\frac{1}{2}$a2bc3•(-2a2b2c)2(2)(x+1)2-(3+x)(x-3)
(3)(54x2y-108xy2-36xy)÷(18xy)
(4)a2•a3-2a7÷a2
(5)(x-y)(x+y)(x2-y2)
(6)(a-2b+3c)2-(a+2b-3c)2.
分析 (1)先计算乘方,再计算单项式相乘;
(2)先计算完全平方和平方差,再去括号合并即可;
(3)根据多项式除以单项式法则即可得;
(4)先计算单项式的乘法和除法,再合并可得;
(5)先计算平方差,再计算完全平方式;
(6)根据平方差公式因式分解,再利用乘法分配律展开即可得.
解答 解:(1)原式=$\frac{1}{2}$a2bc3•4a4b4c2
=2a6b5c5;
(2)原式=x2+2x+1-(x2-9)
=x2+2x+1-x2+9
=2x+10;
(3)原式=3x-6y-2;
(4)原式=a5-2a5=-a5;
(5)原式=(x2-y2)2=x4-2x2y2+y4;
(6)原式=(a-2b+3c+a+2b-3c)(a-2b+3c-a-2b+3c)
=2a(-4b+6c)
=-8ab+12ac.
点评 此题考查了整式的混合运算,熟练掌握整式混合运算顺序和运算法则及完全平方公式、平方差公式是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
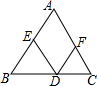 如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.
如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.



 如图,在△ABC中,AB=AC=BC=6,求△ABC外接圆⊙O的半径r.
如图,在△ABC中,AB=AC=BC=6,求△ABC外接圆⊙O的半径r.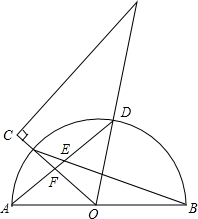 如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.
如图,半圆O中,将一块含60°的直角三角板的60°角顶点与圆心O重合,角的两条边分别与半圆圆弧交于C,D两点(点C在∠AOD内部),AD与BC交于点E,AD与OC交于点F.