题目内容
16.直线y=4x-2与两坐标轴围成的三角形的面积是$\frac{1}{2}$.分析 首先求出直线y=4x-2与x轴、y轴的交点的坐标,然后根据三角形的面积公式,得出结果.
解答 解:令x=0,则y=-2,
令y=0,则x=$\frac{1}{2}$,
故直线y=2x-4与两坐标轴的交点分别为(0,-2)、($\frac{1}{2}$,0),
故直线y=4x-2与两坐标轴围成的三角形面积=$\frac{1}{2}$×|-2|×$\frac{1}{2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查的是一次函数图象上点的坐标特点,会求一次函数y=kx+b与x轴的交点为(-$\frac{b}{k}$,0),与y轴的交点为(0,b)是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
11.下列根式中属最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{{a}^{2}}$ |
1.菱形的周长为4,两个相邻的内角的度数之比为1:2,则较短的对角线为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{1}{2}$ |
5.如果代数式$\frac{x-3}{\sqrt{x-2}}$有意义,那么x的取值范围是( )
| A. | x≥2 | B. | x>2且x≠3 | C. | x>2 | D. | x≥2且x≠3 |
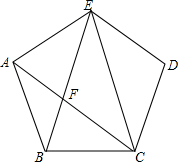 如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$.
如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$.