题目内容
14．解不等式组：$\left\{\begin{array}{l}{3（x+2）≥2x+5，①}\\{2x＞3（x-1），②}\end{array}\right.$，并把它的解集表示在数轴上．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
解答 解：解不等式3（x+2）≥2x+5，得：x≥-1，
解不等式2x＞3（x-1），得：x＜3，
则不等式组的解集为-1≤x＜3，
将解集表示在数轴上如下：
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
5．如图，是用棋子摆成的图案，摆第①个图案需要7枚棋子，摆第②个图案需要12枚棋子，摆第③个图案需要19枚棋子，摆第④个图案需要28枚棋子，…，按照这样的规律，则摆第n个图案需要n2+2n+4枚棋子．
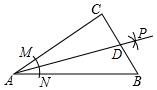如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交边AC、AB于点M、N，再分别以点M、N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=2，AB=6，则△ABD的面积是（ ）
9．下列方程中，一定是一元二次方程的是（ ）
| A． | 2x2-7=3y+1 | B． | 5x2-$\frac{1}{x}$-2=0 | C． | $\frac{1}{3}$x-5=$\frac{{x}^{2}}{2}$ | D． | ax2+bx+c=0 |
现有长方形纸片一张，长19cm，宽15cm，需要剪去边长是多少的小正方形才能做成底面积为77cm2的无盖长方体型的纸盒？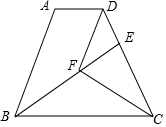
如图，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF的延长线交DC于点E．