题目内容
3.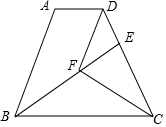 如图,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.
如图,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.(1)求证:△BFC≌△DFC;
(2)已知AD=6,求DE的长.
分析 (1)由CF平分∠BCD可知∠BCF=∠DCF,然后通过SAS就能证出△BFC≌△DFC;
(2)要证明AD=DE,连接BD,证明△BAD≌△BED即可;
解答 证明:(1)∵CF平分∠BCD,
∴∠BCF=∠DCF.
在△BFC和△DFC中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCF=∠DCF}\\{FC=FC}\end{array}\right.$,
∴△BFC≌△DFC(SAS).
(2)连接BD.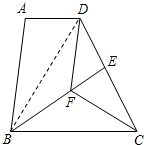
∵△BFC≌△DFC,
∴BF=DF,∴∠FBD=∠FDB.
∵DF∥AB,
∴∠ABD=∠FDB.
∴∠ABD=∠FBD.
∵AD∥BC,
∴∠BDA=∠DBC.
∵BC=DC,
∴∠DBC=∠BDC.
∴∠BDA=∠BDC.
又∵BD是公共边,
∴△BAD≌△BED(ASA).
∴AD=DE,
∵AD=6,
∴DE=6.
点评 本题考查全等三角形的判定和性质、平行线的性质等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

 如图,把Rt△ABC沿BC方向平移得到Rt△DEF,已知AB=8,BC=11,CF=5,DH=3,求图中阴影部分的面积.
如图,把Rt△ABC沿BC方向平移得到Rt△DEF,已知AB=8,BC=11,CF=5,DH=3,求图中阴影部分的面积.