题目内容
 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,作AE∥BC,CE∥AD,AE、CE交于点E.
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,作AE∥BC,CE∥AD,AE、CE交于点E.(1)证明:四边形ADCE是矩形.
(2)若DE交AC于点O,证明:OD∥AB且OD=
| 1 |
| 2 |
考点:矩形的判定与性质,三角形中位线定理
专题:证明题
分析:(1)根据等腰三角形三线合一的性质可得AD⊥BC,且BD=CD,再求出四边形ADCE是平行四边形,然后根据有一个角是直角的平行四边形是矩形;
(2)根据矩形的对角线互相平分可得OA=OC,然后求出OD是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半证明.
(2)根据矩形的对角线互相平分可得OA=OC,然后求出OD是△ABC的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半证明.
解答:证明:(1)∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,且BD=CD,
∵AE∥BC,CE∥AD,
∴四边形ADCE是平行四边形,
∴四边形ADCE是矩形;
(2)∵四边形ADCE是矩形,
∴OA=OC,
∴OD是△ABC的中位线,
∴OD∥AB且OD=
AB.
∴AD⊥BC,且BD=CD,
∵AE∥BC,CE∥AD,
∴四边形ADCE是平行四边形,
∴四边形ADCE是矩形;
(2)∵四边形ADCE是矩形,
∴OA=OC,
∴OD是△ABC的中位线,
∴OD∥AB且OD=
| 1 |
| 2 |
点评:本题考查了矩形的判定与性质,三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,熟记特殊四边形的判定与性质是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
如图几何体中是棱锥的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在正方形ABCD所在的平面内求一点P,使△PAB,△PBC,△PCD,△PAD都是等腰三角形,具有这性质的点P有
如图,在正方形ABCD所在的平面内求一点P,使△PAB,△PBC,△PCD,△PAD都是等腰三角形,具有这性质的点P有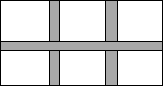 新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为
新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为