题目内容
在半径为1的⊙O中,弦AB=
,半径OC与弦AB所夹的锐角为70°,连接AC,则∠BAC= 度.
| 3 |
考点:垂径定理,特殊角的三角函数值
专题:
分析:连结OA、OB,作OD⊥AB于D,根据垂径定理得出AD=BD=
AB=
,在Rt△OBD中,由正弦函数的定义得到sin∠BOD=
=
,根据特殊角的三角函数值得到∠BOD=60°,于是由三角形内角和定理求出∠B=30°,根据三角形外角的性质得到∠BOC=70°-30°=40°,然后根据圆周角定理求出∠BAC=∠BOC=40°.
| 1 |
| 2 |
| ||
| 2 |
| BD |
| OB |
| ||
| 2 |
解答: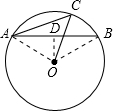 解:如图,连结OA、OB,作OD⊥AB于D,则AD=BD=
解:如图,连结OA、OB,作OD⊥AB于D,则AD=BD=
AB=
.
在Rt△OBD中,∵∠ODB=90°,
∴sin∠BOD=
=
=
,
∴∠BOD=60°,
∴∠B=30°,
∴∠BOC=70°-30°=40°,
∴∠BAC=∠BOC=40°.
故答案为40.
 解:如图,连结OA、OB,作OD⊥AB于D,则AD=BD=
解:如图,连结OA、OB,作OD⊥AB于D,则AD=BD=| 1 |
| 2 |
| ||
| 2 |
在Rt△OBD中,∵∠ODB=90°,
∴sin∠BOD=
| BD |
| OB |
| ||||
| 1 |
| ||
| 2 |
∴∠BOD=60°,
∴∠B=30°,
∴∠BOC=70°-30°=40°,
∴∠BAC=∠BOC=40°.
故答案为40.
点评:本题考查了垂径定理,正弦函数的定义,特殊角的三角函数值,三角形内角和定理,三角形外角的性质,圆周角定理,涉及的知识点较多,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
相关题目

 如图,∠AOB=164°59′58″,∠AOC=∠BOD=90°,求∠COD的度数(结果用度,分,秒表示)
如图,∠AOB=164°59′58″,∠AOC=∠BOD=90°,求∠COD的度数(结果用度,分,秒表示)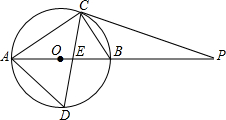 如图,⊙O的直径AB为10,弦BC为6,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE
如图,⊙O的直径AB为10,弦BC为6,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE