题目内容
8．从-1，0，$\frac{1}{3}$，π，3，这5个数中随机抽取一个，取到无理数的概率是$\frac{1}{5}$．分析 由题意可得共有5种等可能的结果，其中无理数只有π共1种情况，则可利用概率公式求解．
解答 解：∵共有5种等可能的结果，无理数有：只有π共1种情况，
∴取到无理数的概率是：$\frac{1}{5}$．
故答案为：$\frac{1}{5}$．
点评 此题考查了概率公式的应用与无理数的定义．此题比较简单，注意用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
18．若x1，x2是一元二次方程x2-2x-3=0的两个根，则x1，x2的值是（ ）
| A． | -1，-3 | B． | 1，3 | C． | 1，-3 | D． | -1，3 |
19．
如图一个矩形减去一个以宽为边长的正方形后，所剩下的矩形与原矩形相似，则原矩形的长与宽的比值为（ ）
如图一个矩形减去一个以宽为边长的正方形后，所剩下的矩形与原矩形相似，则原矩形的长与宽的比值为（ ）| A． | $\frac{{3+\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{5}-1}}{2}$ | C． | $\frac{{3-\sqrt{5}}}{2}$ | D． | $\frac{{\sqrt{5}+1}}{2}$ |
16．已知x1=5，x2=-5是一元二次方程x2+ax+b=0的两个根，则a，b的值为（ ）
| A． | a=25，b=-25 | B． | a=0，b=-25 | C． | a=25，b=25 | D． | a=0，b=25 |
17．
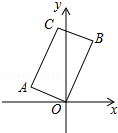如图，在矩形AOBC中，点A的坐标是（-2，1），点C的纵坐标是4，则B、C两点的坐标分别是（ ）
如图，在矩形AOBC中，点A的坐标是（-2，1），点C的纵坐标是4，则B、C两点的坐标分别是（ ）| A． | （$\frac{3}{2}$，3）、（-$\frac{2}{3}$，4） | B． | （$\frac{7}{4}，\frac{7}{2}$）、（-$\frac{1}{2}，4$） | C． | （$\frac{7}{4}，\frac{7}{2}$）、（-$\frac{2}{3}，4$） | D． | （$\frac{3}{2}，3$）、（-$\frac{1}{2}，4$） |
