题目内容
11．
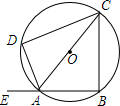如图，在⊙O中，弦AB的长等于半径，点E在BA的延长线上，∠DAE=80°，则∠ACD=50°．
分析 连结OB，如图，先判断△OAB为等边三角形得到∠AOB=60°，再根据圆周角定理得到∠ACB=$\frac{1}{2}∠$AOB=30°，然后利用圆内接四边形的性质得∠DAE=∠BCD=80°，于是得到∠ACD=50°．
解答 解：连结OB，如图，
∵AB=OB=OA，
∴△OAB为等边三角形，
∴∠AOB=60°，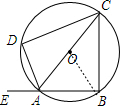
∴∠ACB=$\frac{1}{2}∠$AOB=30°，
∵∠DAE=∠BCD=80°，
∴∠ACD=80°-30°=50°．
故答案为50°．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了等边三角形的判定与性质．
练习册系列答案
名校课堂系列答案
相关题目
1．小冬记录了今年雨季某市一周内的水位变化情况（上周末水位达到警戒水位73.4m）．
（1）本周哪一天的水位最高？哪一天的水位最低？
（2）与上周相比，本周末的水位是上升了，还是下降了？在讨论这个问题时，各小组的意见不一．
第一小组认为：本周二水位最高，星期六水位最低，因为+0.81最大，而-0.36最小；
第二小组认为：本周一水位最低，因为水位都是在前一天基础上进行变化的；
第三小组认为：因为星期日水位在星期六的水位上又变化了-0.01m，星期日水位最低，星期二水位最高；
第四小组认为：无法确定哪一天水位最高或最低；
如果你也参加了讨论，你怎么看待这个问题？
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 与前一天水位的差/m | +0.20 | +0.81 | -0.35 | +0.03 | +0.28 | -0.36 | -0.01 |
（2）与上周相比，本周末的水位是上升了，还是下降了？在讨论这个问题时，各小组的意见不一．
第一小组认为：本周二水位最高，星期六水位最低，因为+0.81最大，而-0.36最小；
第二小组认为：本周一水位最低，因为水位都是在前一天基础上进行变化的；
第三小组认为：因为星期日水位在星期六的水位上又变化了-0.01m，星期日水位最低，星期二水位最高；
第四小组认为：无法确定哪一天水位最高或最低；
如果你也参加了讨论，你怎么看待这个问题？