若非零实数m.n满足m=0.则分式$\frac{{{m^2}+1}}{{{m^2}-2mn}}-\frac{1}{2mn}$的值为( )A．$\frac{1}{2}$B．1C．2D．$\frac{1}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

18．若非零实数m，n满足m（m-4n）=0，则分式$\frac{{{m^2}+1}}{{{m^2}-2mn}}-\frac{1}{2mn}$的值为（　　）

A．

$\frac{1}{2}$

B．

C．

D．

$\frac{1}{3}$

分析已知等式整理得到m=4n，代入原式计算即可得到结果．

解答解：∵m（m-4n）=0，
∴m=0（舍去）或m=4n，
则原式=$\frac{16{n}^{2}+1}{16{n}^{2}-8{n}^{2}}$-$\frac{1}{8{n}^{2}}$=$\frac{16{n}^{2}}{8{n}^{2}}$=2，
故选C．

点评此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案

相关题目

8．

如图，四边形ABCD是平行四边形，以AB为直径的⊙0经过点D，E是⊙O上一点，且∠AED=45°，
（1）求证：CD是⊙O的切线．
（2）若⊙O的半径为3，AE=5，求∠ADE的正弦值．

9．学校象棋小组进行象棋比赛，每两人比赛一场，一共进行了45场比赛，若设象棋小组有x名学生，则根据题意可列方程（　　）

$\frac{1}{2}$x（x-1）=45

D．

$\frac{1}{2}$x（x+1）=45

6．

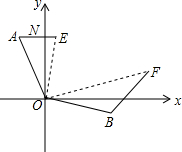如图，在一次海关缉私行动中，发现一走私艇在海关指挥艇（O处）北偏西30°的A处，此时缉私艇在指挥艇南偏东70°的B处，并且两船到指挥艇的距离相等，现发现走私艇向正东方向以30海里/小时的速度前进，与此同时缉私艇沿北偏东50°的方向以40海里/小时的速度前进1小时后，指挥艇观测走私艇，缉私艇分别到达E，F处，这时两船的夹角∠EOF=70°，试求此时两船之间的距离．

13．

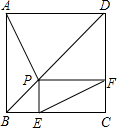如图，点P为正方形ABCD对角线BD上一点，PE⊥BC于E，PF⊥DC于F．
（1）求证：PA=EF；
（2）若正方形ABCD的边长为a，求四边形PFCE的周长．

3．一旅游团50人到一旅社住宿，旅社的客房有三人间，双人间，单人间三种，其中住三人间的没人每晚付20元，住双人间的每人每晚付30元，住单人间的每人每晚付50元．
（1）若旅游团共住满了20间客房，问三种客房各住了几间？怎样住消费最低？
（2）若该旅游团中，是一对夫妻的住双人间，是单身的住三人间，小孩可随父母住在一起，现已知有小孩4人（每对夫妻最多只有1个小孩，无单身成人带小孩），单身的30人，其中男性17人，另有两名单身心脏病患者要求住单人间，问这一行人共需多少间客房？

10．

7．计算：$\frac{x-3}{{x}^{2}+3x+2}$•$\frac{{x}^{2}}{{x}^{2}-4x+3}$．

8．在实数0，-$\sqrt{3}$，-$\frac{2}{3}$，|-2|中，最小的数是（　　）

试题分类