计算:$\frac{x-3}{{x}^{2}+3x+2}$•$\frac{{x}^{2}}{{x}^{2}-4x+3}$．题目和参考答案——青夏教育精英家教网—

题目内容

7．计算：$\frac{x-3}{{x}^{2}+3x+2}$•$\frac{{x}^{2}}{{x}^{2}-4x+3}$．

分析先利用因式分解后，再根据分式的乘除进行计算即可．

解答解：$\frac{x-3}{{x}^{2}+3x+2}$•$\frac{{x}^{2}}{{x}^{2}-4x+3}$
=$\frac{x-3}{（x+2）（x+1）}•\frac{{x}^{2}}{（x-3）（x-1）}$
=$\frac{{x}^{2}}{（x+2）（{x}^{2}-1）}$

点评此题考查分式的乘除，关键是把分式进行因式分解后化简计算．

练习册系列答案

18．若非零实数m，n满足m（m-4n）=0，则分式$\frac{{{m^2}+1}}{{{m^2}-2mn}}-\frac{1}{2mn}$的值为（　　）

15．某手机超市举办黄金周买手机抽大奖活动，奖品分为一等奖-四等奖，四个等级中奖率100%，现从一周购买手机的人中任意选取若干人对其中奖情况进行调查，结果如下统计图，根据图中信息解答下列问题：
（1）此次调查共抽取了300人；
（2）补全条形统计图，并求出“二等奖”获奖人数在扇形统计图中所占圆心角的度数．
（3）若一周共1000人购买手机，请估计中“二等奖”和“三等奖”人数共有多少？

2．已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=k}\\{2x-y=5k}\end{array}\right.$的解也是方程4x-y=18的解，求k的值．

12．

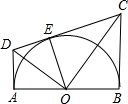如图，AB为半圆O的直径，AD、BC分别切⊙O于A，B两点，CD切⊙O于点E，AD与CD相交于D，BC与CD相交于C，连结OD、OE、OC，对于下列结论：
①AD+BC=CD；②∠DOC=90°；③S_梯形ABCD=$\frac{1}{2}$CD•OA；④$\frac{OD}{DE}=\frac{CD}{OD}$．
其中结论正确的个数是（　　）

19．

已知点A、B和直线l，求作：点P，使点P在直线l上，且PA=PB．

16．下列各组数的大小比较中，正确的是（　　）

17．计算：$\sqrt{\frac{1}{16}}$+2^-2=$\frac{1}{2}$．

试题分类