题目内容
14.数学活动-探究线段之间的关系.问题情境:活动课上,小颖向同学们提出一个问题:如图1,在正方形ABCD中,点E,F分别在BA,DA的延长线上,且AE=AF,连接EF,BF,DE,M是DE的中点,连接AM.判断线段AM与BF之间的数量关系.并说明理由.
独立思考:
(1)请你解答小颖提出的问题
合作交流:
(2)解决完(1)之后,小彬将△AEF从图1的位置开始绕点A顺时针旋转(其余条件不变),当旋转角小于90°时(如图2),小彬猜想(1)中的结论仍然成立.为证明这一猜想,同学们展开讨论,大家发现需要构造与AM,BF有关的“新”线段.请你参考同学们的思路证明小彬的猜想.
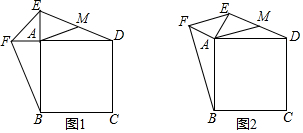
分析 (1)根据正方形的性质得到AB=AD,∠DAB=∠FAB=∠EAD=90°,根据全等三角形的性质得到BF=DE,根据直角三角形的性质即可得到结论;
(2)如图2,延长AM到G,使AM=MG,连接EG,推出四边形EADG是平行四边形,根据平行四边形的性质得到DG=AE=AF,∠EAD+∠ADG=180°,根据全等三角形的性质即可得到结论.
解答 解:(1)结论:AM=$\frac{1}{2}$BF.
理由:∵四边形ABCD是正方形,
∴AB=AD,∠DAB=∠FAB=∠EAD=90°,
在△ABF和△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠EAD}\\{AF=AE}\end{array}\right.$,
∴△ABF≌△ADE,
∴BF=DE,
在Rt△AED中,∵EM=MD,
∴AM=$\frac{1}{2}$DE,
∴AM=$\frac{1}{2}$BF;
(2)如图2,延长AM到G,使AM=MG,连接EG,
∵EM=MD,AM=MG,
∴四边形EADG是平行四边形,
∴DG=AE=AF,∠EAD+∠ADG=180°,AM=$\frac{1}{2}$AG,
∵∠FAB+∠EAD=180°,
∴∠FAB=∠ADG,
在△FAB与△GDA中,$\left\{\begin{array}{l}{AB=AD}\\{∠FAB=∠ADG}\\{DG=AF}\end{array}\right.$,
∴△FAB≌△GDA,
∴AG=FB,
∴AM=$\frac{1}{2}$BF.
点评 本题考查了旋转的性质,正方形的性质,全等三角形的判定和性质,平行四边形的判定和性质,正确的作出辅助线是解题的关键,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.在一个不透明的袋中,有若干个白色乒乓球和4个黄色乒乓球,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回袋中,通过大量重复摸球实验后发现,摸到黄球的频率稳定在40%,那么,估计袋中白色乒乓球的个数为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
19.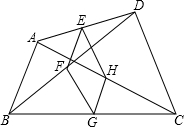 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
 如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )
如图,点E,F,G,H分别是任意四边形ABCD中AD,BD,CA,BC的中点.若四边形EFCH是菱形,则四边形ABCD的边需满足的条件是( )| A. | AB∥DC | B. | AC=BD | C. | AC⊥BD | D. | AB=DC |
6.下列计算正确的是( )
| A. | a4+a2=a6 | B. | a2+a2+a2=a6 | C. | a2•a3=a6 | D. | a2•a2•a2=a6 |
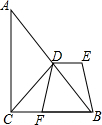 已知:如图,△ABC中,∠ACB=90°,D为AB边中点,点F在BC边上,DE∥CF,且DE=CF.若DF=2,EB的长为2.
已知:如图,△ABC中,∠ACB=90°,D为AB边中点,点F在BC边上,DE∥CF,且DE=CF.若DF=2,EB的长为2. 请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.
请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.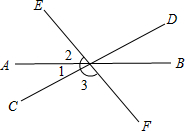 已知:如图,∠2=2∠1,∠3=3∠2,求∠DOE的度数.
已知:如图,∠2=2∠1,∠3=3∠2,求∠DOE的度数.