题目内容
9.在△ABC中,AB=AC,BC=8cm,△ABC的外接圆半径为5,则△ABC的面积是8或32cm2.分析 根据题意画出图形,利用等腰三角形的性质得出AD⊥BC,BD=CD,再由勾股定理求出OD的长,再分BC在⊙O的上方与下方两种情况讨论即可.
解答 解:如图,连接AO,并延长与BC交于一点D,连接OC,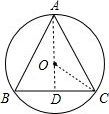
∵BC=8cm,⊙O的半径为5cm,AB=AC,
∴AD⊥BC,
∴CD=$\frac{1}{2}$BC=4,
∴OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AD=3+5=8,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×8×8=32;
同理当BC在圆心O的上方时,三角形的高变为5-3=2,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×8×2=8.
故答案为:8或32.
点评 本题考查的是三角形的外接圆与外心,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目



 如图,从电线杆离地面9m处向地面拉一条长15m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有12m.
如图,从电线杆离地面9m处向地面拉一条长15m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有12m.
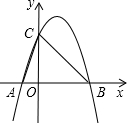 如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
如图,抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.