题目内容
10.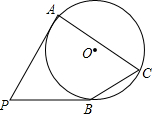 如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )
如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
分析 要求∠ACB的度数,只需根据圆周角定理构造它所对的弧所对的圆心角,即连接OA,OB;再根据切线的性质以及四边形的内角和定理即可求解.
解答  解:连接OA,OB,
解:连接OA,OB,
∵PA,PB是⊙O的切线,
∴PA⊥OA,PB⊥OB,
∴∠AOB=360°-(90°+90°+50°)=130°,
∴∠ACB=$\frac{1}{2}$∠AOB=65°.
故选D.
点评 本题考查了多边形的内角和定理,切线的性质,圆周角定理的应用,关键是求出∠AOB的度数和得出∠ACB=$\frac{1}{2}$∠AOB.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
1.下面是三角形三边的比,其中是直角三角形三边的比的是( )
| A. | 2:1:2 | B. | 2:3:4 | C. | 1:1:$\sqrt{2}$ | D. | 4:5:6 |
15.若$\frac{|x|-2}{{x}^{2}-x-2}$=0,则x等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
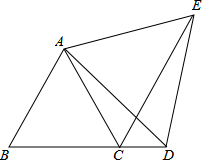 如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.
如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.