题目内容
1.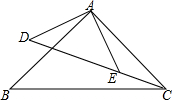 如图,已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,且D、E、C三点在一直线上.若AD=AE=1,DE=2EC,则BC=$\sqrt{5}$.
如图,已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,且D、E、C三点在一直线上.若AD=AE=1,DE=2EC,则BC=$\sqrt{5}$.
分析 连接BD,根据等腰直角三角形的性质得到DE=$\sqrt{2}$AE=$\sqrt{2}$,求得CE=$\frac{\sqrt{2}}{2}$,CD=$\frac{3\sqrt{2}}{2}$,通过△ADB≌△ACE,根据全等三角形的性质得到BD=CE=$\frac{\sqrt{2}}{2}$,∠AEC=∠ADB,求得∠BDC=90°,由勾股定理即可得到结论.
解答 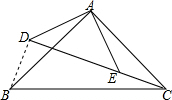 解:连接BD,
解:连接BD,
∵△ADE为等腰直角三角形,
∴DE=$\sqrt{2}$AE=$\sqrt{2}$,
∵DE=2EC,
∴CE=$\frac{\sqrt{2}}{2}$,
∴CD=$\frac{3\sqrt{2}}{2}$,
∵∠BAC=∠DAE=90°,
∴∠DAB=90°-∠BAE,∠CAE=90°-∠BAE,
∴∠DAB=∠CAE,
在△ADB与△ACE中,
$\left\{\begin{array}{l}{AD=AE}\\{∠DAB=∠EAC}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△ACE,
∴BD=CE=$\frac{\sqrt{2}}{2}$,∠AEC=∠ADB,
∵∠AEC=135°,
∴∠ADB=135°,
∴∠BDC=90°,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=$\sqrt{(\frac{\sqrt{2}}{2})^{2}+(\frac{3\sqrt{2}}{2})^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.已知,在△ABC中,AB=8cm,AC=4cm,AD是BC边上的中线,则中线AD长度的取值范围是( )
| A. | 4<AD<12 | B. | 2<AD<6 | C. | 4<AD<8 | D. | 2<AD<12 |
16.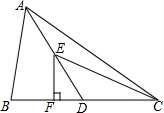 在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
 在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )| A. | 1.2 | B. | 2.4 | C. | 3.6 | D. | 4.8 |
10.把抛物线y=2x2向左平移3个单位,再向上平移2个单位所得抛物线的解析式为( )
| A. | y=2(x+3)2+2 | B. | y=2(x-2)2+3 | C. | y=2(x+2)2+3 | D. | y=2(x-3)2+2 |
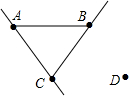 如图所示,按要求画图.
如图所示,按要求画图. 实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入$\frac{5}{3}$或$\frac{20}{3}$分钟水量后,甲的水位比乙高1cm.
实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入$\frac{5}{3}$或$\frac{20}{3}$分钟水量后,甲的水位比乙高1cm.