题目内容
9.已知,在△ABC中,AB=8cm,AC=4cm,AD是BC边上的中线,则中线AD长度的取值范围是( )| A. | 4<AD<12 | B. | 2<AD<6 | C. | 4<AD<8 | D. | 2<AD<12 |
分析 延长AD到E,使AD=DE,连接BE,证△ADC≌△EDB,推出AC=BE=8,在△ABE中,根据三角形三边关系定理得出AB-BE<AE<AB+BE,代入求出即可.
解答 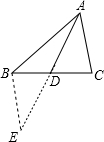 解:延长AD到E,使AD=DE,连接BE,
解:延长AD到E,使AD=DE,连接BE,
∵AD是BC边上的中线,
∴BD=CD,
在△ADC和△EDB中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADC=∠EDB}\\{DC=BD}\end{array}\right.$,
∴△ADC≌△EDB(SAS),
∴AC=BE=4,
在△ABE中,AB-BE<AE<AB+BE,
∴8-4<2AD<8+4,
∴2<AD<6,
故选B.
点评 本题考查了全等三角形的性质和判定,三角形的三边关系定理的应用,主要考查学生的推理能力.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
4.现有2cm,4cm,5cm,8cm,9cm长的五根木棒,任意选取三根组成一个三角形,选法种数有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
14. 若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )
若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )
 若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )
若反比例函数y1=$\frac{k}{x}$的图象和一次函数y2=ax+b的图象如图所示,则当y1<y2时,相应的x的取值范围是( )| A. | -5<x<-1或x>0 | B. | x<-5或x>-1 | C. | -5<x<-1 | D. | x<-5或-1<x<0 |
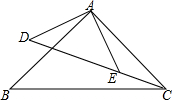 如图,已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,且D、E、C三点在一直线上.若AD=AE=1,DE=2EC,则BC=$\sqrt{5}$.
如图,已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,且D、E、C三点在一直线上.若AD=AE=1,DE=2EC,则BC=$\sqrt{5}$.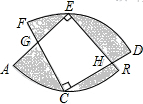 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.