题目内容
17.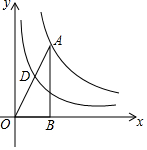 如图,已知点A在双曲线y=$\frac{8}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点D,若OD=AD,则k的值为2.
如图,已知点A在双曲线y=$\frac{8}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点D,若OD=AD,则k的值为2.
分析 设A(x,y),根据点A在双曲线y=$\frac{8}{x}$上得出xy=8.由OD=AD,得出D是线段OA的中点,利用线段中点坐标公式得到D($\frac{1}{2}$x,$\frac{1}{2}$y),由双曲线y=$\frac{k}{x}$过点D,得出k=$\frac{1}{2}$x•$\frac{1}{2}$y=2.
解答 解:设A(x,y),则xy=8.
∵OD=AD,
∴D是线段OA的中点,
∴D($\frac{1}{2}$x,$\frac{1}{2}$y),
∵双曲线y=$\frac{k}{x}$过点D,
∴k=$\frac{1}{2}$x•$\frac{1}{2}$y=$\frac{1}{4}$xy=$\frac{1}{4}$×8=2.
故答案为2.
点评 本题考查了反比例函数图象上点的坐标特征,点在图象上,那么点的坐标满足函数解析式.也考查了线段的中点坐标公式.得出D点坐标是解题的关键.

练习册系列答案
相关题目
12.已知菱形ABCD,对角线AC=5,BD=12,则菱形的面积为( )
| A. | 60 | B. | 50 | C. | 40 | D. | 30 |
7.$\sqrt{\frac{1}{16}}$的平方根是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | ±$\frac{1}{4}$ | D. | ±$\frac{1}{2}$ |
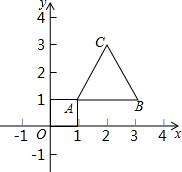 如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2017次变换后,等边△ABC的顶点C的坐标为(-2015,-$\sqrt{3}$-1).
如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,如果这样连续经过2017次变换后,等边△ABC的顶点C的坐标为(-2015,-$\sqrt{3}$-1).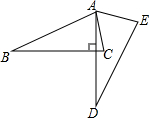 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若AD⊥BC,∠CAE=65°,∠E=70°,则∠BAC的大小为85度.
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若AD⊥BC,∠CAE=65°,∠E=70°,则∠BAC的大小为85度.