题目内容
2.若△ABC∽△DEF,请写出1个正确的结论:答案不唯一,如:∠A=∠D,∠B=∠E,∠C=∠F,$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$等.分析 根据相似三角形的性质:对应角相等,对应边的比相等;写一个结论即可.
解答 解:答案不唯一,如:∠A=∠D,∠B=∠E,∠C=∠F,$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$等;
故答案为:答案不唯一,如:∠A=∠D,∠B=∠E,∠C=∠F,$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$等.
点评 本题考查了相似三角形的性质,属于基础题,熟练掌握相似三角形的性质:对应角相等,对应边的比相等.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
13.已知变量s与t的关系式是s=6t-$\frac{5}{2}$t2,则当t=2时,s=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{mx+ny=8}\\{nx-my=1}\end{array}\right.$的解,则2m+n的立方根为( )
| A. | 4 | B. | 2 | C. | $\sqrt{2}$ | D. | ±2 |
11.下列各式,能用平方差公式计算的是( )
| A. | (a+b)(-a-b) | B. | (a+b)(-a+b) | C. | (-a+b)(a-b) | D. | (-a+b)(b-a) |
12.下列计算正确的是( )
| A. | 3a+2a=6a | B. | a3•a2=a6 | C. | (a3)2=a5 | D. | a3÷a2=a |
 如图,直线AB,CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC的度数为135°.
如图,直线AB,CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC的度数为135°.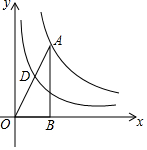 如图,已知点A在双曲线y=$\frac{8}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点D,若OD=AD,则k的值为2.
如图,已知点A在双曲线y=$\frac{8}{x}$上,AB⊥x轴于点B,连接OA交双曲线y=$\frac{k}{x}$于点D,若OD=AD,则k的值为2.
 如图,AB∥CD,若∠ECD=54°,则∠EAB的度数为54°.
如图,AB∥CD,若∠ECD=54°,则∠EAB的度数为54°.