题目内容
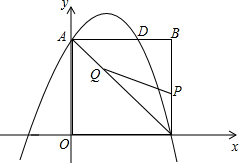 如图,已知,在平面直角坐标系内,点B的坐标为(6,8),过点B分别向x轴和y轴作垂线,垂足分别为C、A,抛物线y=-
如图,已知,在平面直角坐标系内,点B的坐标为(6,8),过点B分别向x轴和y轴作垂线,垂足分别为C、A,抛物线y=-| 4 |
| 9 |
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
(3)①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线y=-
| 4 |
| 9 |
考点:二次函数综合题
专题:
分析:(1)将A、C两点坐标代入抛物线y=-
x2+bx+c,即可求得抛物线的解析式;
(2)①先用m表示出QE的长度,进而求出三角形的面积S关于m的函数,配方后即可确定最大值;
②直接写出满足条件的F点的坐标即可,注意不要漏写.
| 4 |
| 9 |
(2)①先用m表示出QE的长度,进而求出三角形的面积S关于m的函数,配方后即可确定最大值;
②直接写出满足条件的F点的坐标即可,注意不要漏写.
解答:解:(1)∵点B的坐标为(6,8),过点B分别向x轴和y轴作垂线,垂足分别为C、A,
∴点A的坐标为(0,8),点C的坐标为(6,0),
∴将A、C两点坐标代入抛物线,得
,
解得:
,
∴抛物线的解析式为y=-
x2+
x+8;
(2)①∵OA=8,OC=6 ,
,
∴AC═10,
过点Q作QE⊥BC与E点,则sin∠ACB=
=
=
,
∴
=
,
∴QE=
(10-m),
∴S=
•CP•QE=
m×
(10-m)=-
m2+3m=-
(m-5)2+
,
∴当m=5时,有最大面积;
②在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=-
x2+
x+8的对称轴为x=
,
D的坐标为(3,8),Q(3,4),
当∠FDQ=90°时,F1(
,8),
当∠FQD=90°时,则F2(
,4),
当∠DFQ=90°时,设F(
,n),
则FD2+FQ2=DQ2,
即
+(8-n)2+
+(n-4)2=16,
解得:n=6±
,
∴F3(
,6+
),F4(
,6-
),
满足条件的点F共有四个,坐标分别为
F1(
,8),F2(
,4),F3(
,6+
),F4(
,6-
).
∴点A的坐标为(0,8),点C的坐标为(6,0),
∴将A、C两点坐标代入抛物线,得
|
解得:
|
∴抛物线的解析式为y=-
| 4 |
| 9 |
| 4 |
| 3 |
(2)①∵OA=8,OC=6
 ,
,∴AC═10,
过点Q作QE⊥BC与E点,则sin∠ACB=
| QE |
| QC |
| AB |
| AC |
| 3 |
| 5 |
∴
| QE |
| 10-m |
| 3 |
| 5 |
∴QE=
| 3 |
| 5 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 3 |
| 10 |
| 15 |
| 2 |
∴当m=5时,有最大面积;
②在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=-
| 4 |
| 9 |
| 4 |
| 3 |
| 3 |
| 2 |
D的坐标为(3,8),Q(3,4),
当∠FDQ=90°时,F1(
| 3 |
| 2 |
当∠FQD=90°时,则F2(
| 3 |
| 2 |
当∠DFQ=90°时,设F(
| 3 |
| 2 |
则FD2+FQ2=DQ2,
即
| 9 |
| 4 |
| 9 |
| 4 |
解得:n=6±
| ||
| 2 |
∴F3(
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
满足条件的点F共有四个,坐标分别为
F1(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
点评:本题是二次函数的综合题,其中涉及到的知识点有抛物线的解析式的求法抛物线的最值等知识点,是各地中考的热点和难点,解题时注意数形结合数学思想的运用,同学们要加强训练,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
下列命题中,正确的是( )
| A、相等的角是对顶角 |
| B、等腰三角形都相似 |
| C、位似图形上任意一对对应点到位似中心的距离之比等于位似比 |
| D、对角线互相垂直平分的四边形是正方形 |

 已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0),B(-2,0),C(0,-2),直线x=m(m<-2)与x轴交于点D.
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0),B(-2,0),C(0,-2),直线x=m(m<-2)与x轴交于点D. 如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.
如图,小丽想知道自家门前小河的宽度,于是她按以下办法测出了如下数据:小丽在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°;小丽沿岸向前走30m选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小丽计算小河的宽度.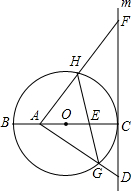 如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.
如图,⊙O的直径BC=8,过点C作⊙O的切线m,D是直线m上一点,且DC=4,A是线段BO上一动点,连结AD交⊙O于点G,过点A作AF⊥AD交直线m于点F,交⊙O于点H,连结GH交BC于点E.