题目内容
14.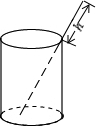 将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,如图,设筷子露在杯子外面的长度为h cm,则h的取值范围是( )| A. | h≤17 | B. | 7≤h≤16 | C. | 15≤h≤16 | D. | h≥8 |
分析 如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.
解答 解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24-8=16cm;
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=15,BD=8,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=17,
∴此时h=24-17=7cm,
所以h的取值范围是7cm≤h≤16cm.
故选B.
点评 本题考查了勾股定理的应用,能够读懂题意和求出h的值最大值与最小值是解题关键.

练习册系列答案
相关题目
4.已知等腰三角形的两边长是5cm和6cm,则此三角形的周长是( )
| A. | 16cm | B. | 17cm | C. | 11cm | D. | 16cm或17cm |