题目内容
2．
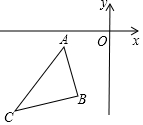如图，在平面直角坐标系中，点A（-3，-1）、B（-2，-4）、C（-6，-5），以原点位似中心将△ABC缩小，位似比为1：2，则点B的对应点的坐标为（-1，-2）或（1，2）．
分析 利用位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k，把B点的横纵坐标都乘以$\frac{1}{2}$或-$\frac{1}{2}$即可得到点B的对应点的坐标．
解答 解：∵以原点位似中心将△ABC缩小，位似比为1：2，
∴点B的对应点的坐标为（-1，-2）或（1，2）．
故答案为（-1，-2）或（1，2）．
点评 本题考查了位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．
练习册系列答案
相关题目
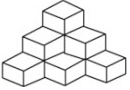把若干个棱长为a的立方体摆成如图形状：从上向下数，摆一层有1个立方体，摆二层共有4个立方体，摆三层共有10个立方体，那么摆五层共有35个立方体．
10．设三角形三边之长分别为3，8，1-2a，则a的取值范围为（ ）
| A． | -6＜a＜-3 | B． | -5＜a＜-2 | C． | -2＜a＜5 | D． | a＜-5或a＞2 |
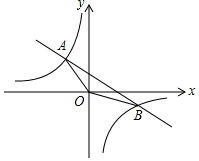如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=$\frac{n}{x}$的图象相交于A（-1，2），B（2，m）两点，连接OA，OB．