题目内容
12.解不等式 (组),并把解集在数轴上表示出来:(1)2(x-1)-3≤1
(2)$\left\{\begin{array}{l}x-2>0\\ 2({x+1})≥3x-1.\end{array}\right.$.
分析 (1)根据解一元一次不等式的步骤,求出不等式的解集,然后在数轴上表示出来即可.
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集,然后在数轴上表示出来即可.
解答 解:(1)2(x-1)-3≤1
2x-2-3≤1,
2x≤1+2+3,
2x≤6,
x≤3;
把x≤3在数轴上表示出来:
(2)$\left\{\begin{array}{l}{x-2>0①}\\{2(x+1)≥3x-1②}\end{array}\right.$
由①得,x>2;
由②得:x≤3.
∴不等式组的解集是:2<x≤3.
点评 本题主要考查解一元一次不等式,并在坐标轴上表示出来,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若a2的算术平方根是4,则a为( )
| A. | 16 | B. | 4 | C. | ±2 | D. | ±4 |
1.受中日钓鱼岛事件的影响,在钓鱼岛被“国有化”的9月份,某日本品牌食用油价格开始回落,食用油批发商批发这种品牌的食用油,每桶在9月份前四周每周的平均销售价格变化如下表:
进入10月份后,由于受中日关系趋于缓和等因素的影响,食用油的价格开始回升,该品牌食用油销售价格y2(元/桶)从10月份第1周的54元/桶,上升至第2周的57元/桶,且销售价格y2(元/桶)与周数x(x为整数)的变化情况满足二次函数:y2=-$\frac{1}{4}$x2+bx+c.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了3a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上降价a%进行销售,这样顺利的完成了第三周销售1200桶的任务,且获利12000元,请你参考以下数据,估算出a的整数值(0<a<15).
(参考数据:912=8281,922=9464,932=8649,942=8836)
| 周数x | 1 | 2 | 3 | 4 |
| 价格y1(元/桶) | 60 | 59 | 58 | 57 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了3a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上降价a%进行销售,这样顺利的完成了第三周销售1200桶的任务,且获利12000元,请你参考以下数据,估算出a的整数值(0<a<15).
(参考数据:912=8281,922=9464,932=8649,942=8836)
 已知正方体的边长为a.
已知正方体的边长为a.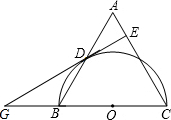 如图,△ABC中,CA=CB,以BC为直径的半圆O交于AB于D,DE⊥AC于E.求证:DE是半圆O的切线.
如图,△ABC中,CA=CB,以BC为直径的半圆O交于AB于D,DE⊥AC于E.求证:DE是半圆O的切线.