题目内容
20.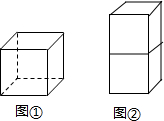 已知正方体的边长为a.
已知正方体的边长为a.(1)一个正方体的表面积是多少?体积是多少?
(2)2个正方体(如图②)叠放在一起,它的表面积是多少?体积是多少?
(3)n个正方体按照图②的方式叠放在一起,它的表面积是多少?体积是多少?
分析 (1)根据正方体的表面积由6个正方形的面积组成,所以正方体的表面积=6×正方形的面积=6a2,正方体的体积=正方体的边长3,把相关数值代入即可求解;
(2)根据(1)的计算结果计算即可;
(3)根据(1)、(2)的计算结果计算即可.
解答 解:(1)依题意得:正方体的表面积=6×正方形的面积=×26a2,体积=a3;
(2)2个正方体叠放在一起,它的表面积=6a2×2-2a2=10a2,体积=2a3;
(3)n个正方体的方式叠放在一起,它的表面积=n•6a2-(n-1)•2a2=(4n+2)a2,体积=na3.
点评 本题考查了几何体的表面积,明确正方体的表面积、体积计算公式,是解答此题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
11.下列关系式中,属于二次函数的是(x是自变量)( )
| A. | y=$\frac{1}{3}{x}^{2}$ | B. | y=$\sqrt{{x}^{2}-1}$ | C. | y=$\frac{1}{{x}^{2}}$ | D. | y=ax2+bx+c |
8. 图中几何体的截面的形状图是( )
图中几何体的截面的形状图是( )
 图中几何体的截面的形状图是( )
图中几何体的截面的形状图是( )| A. |  | B. |  | C. |  | D. |  |
9.下列说法正确的是( )
| A. | 三角形的角平分线、中线、高都在三角形的内部 | |
| B. | 三角形的角平分线、高都在三角形的内部 | |
| C. | 三角形的高、中线都在三角形的内部 | |
| D. | 三角形的角平分线、中线都在三角形的内部 |
10.函数$y=x|x|-2\sqrt{3}x+2$的图象与x轴的交点个数是( )
| A. | 4 | B. | 3 | C. | 1 | D. | 0 |