题目内容
8.计算:$\frac{\frac{1}{2}}{1+\frac{1}{2}}$+$\frac{\frac{1}{3}}{(1+\frac{1}{2})(1+\frac{1}{3})}$+$\frac{\frac{1}{4}}{(1+\frac{1}{2})(1+\frac{1}{3})(1+\frac{1}{4})}$+…+$\frac{\frac{1}{1999}}{(1+\frac{1}{2})(1+\frac{1}{3})(1+\frac{1}{4})+…+(1+\frac{1}{1999})}$.
分析 原式括号中两项通分并利用同分母分数的加法法则计算,约分整理后将各自的分母求和,利用拆项法变形后,计算即可得到结果.
解答 解:原式=$\frac{\frac{1}{2}}{\frac{3}{2}}$+$\frac{\frac{1}{3}}{\frac{3}{2}×\frac{4}{3}}$+$\frac{\frac{1}{4}}{\frac{3}{2}×\frac{4}{3}×\frac{5}{4}}$+…+$\frac{\frac{1}{1999}}{\frac{3}{2}×\frac{4}{3}×\frac{5}{4}×…×\frac{2000}{1999}}$
=$\frac{1}{3}$+$\frac{1}{6}$+$\frac{1}{10}$+…+$\frac{1}{1999000}$
=$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+$\frac{1}{1+2+3+4}$+$\frac{1}{1+2+3+4+5}$+…+$\frac{1}{1+2+…+1999}$
=$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+$\frac{2}{4×5}$+…+$\frac{2}{1998×1999}$
=2×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{1998}$-$\frac{1}{1999}$)
=2×(1-$\frac{1}{1999}$)
=2×$\frac{1998}{1999}$
=$\frac{3996}{1999}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案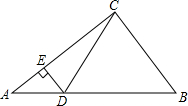 如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$.
如图,在Rt△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,点D,E分别在边AB,AC上,DE⊥AC,DE=6,DB=20,则tan∠BCD的值是$\frac{8}{3}$. 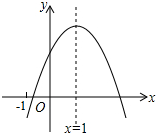 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )| A. | abc<0 | B. | 2a+b=0 | C. | b2-4ac>0 | D. | a-b+c>0 |
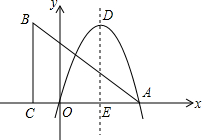 如图,在直角坐标系中,点A,C在x轴上,且AC=8,AB=10,∠ACB=90°
如图,在直角坐标系中,点A,C在x轴上,且AC=8,AB=10,∠ACB=90°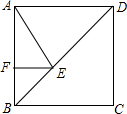 如图,正方形ABCD的边长为4+2$\sqrt{2}$,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是2.
如图,正方形ABCD的边长为4+2$\sqrt{2}$,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长是2.