题目内容
计算:
(1)(
+
)÷
×
;
(2)若实数a,b满足a=
+
+2,求(-1)a-b.
(1)(
| 54 |
|
| 6 |
| 12 |
(2)若实数a,b满足a=
| b-3 |
| 3-b |
考点:二次根式的混合运算,二次根式有意义的条件
专题:计算题
分析:(1)先把各二次根式化为最简二次根式,再把括号内合并,然后进行约分即可;
(2)根据二次根式有意义的条件得到b=3,则可求出a,然后计算(-1)a-b.
(2)根据二次根式有意义的条件得到b=3,则可求出a,然后计算(-1)a-b.
解答:解:(1)原式=(3
+
)×
×2
=
×
×2
=7
;
(2)∵b-3≥0且3-b≥0,
∴b=3,
∴a=2,
∴(-1)a-b=(-1)2•3=1.
| 6 |
| ||
| 2 |
| 1 | ||
|
| 3 |
=
7
| ||
| 2 |
| 1 | ||
|
| 3 |
=7
| 3 |
(2)∵b-3≥0且3-b≥0,
∴b=3,
∴a=2,
∴(-1)a-b=(-1)2•3=1.
点评:本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了二次根式有意义的条件.

练习册系列答案
相关题目
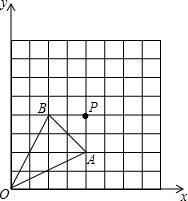 △OAB在坐标系中的位置如图所示.
△OAB在坐标系中的位置如图所示. 如图,AB=AC,DE垂直平分AB,且交AB于点D,交AC于点E.已知BC=2,△BCE的周长为6,求△ABC的周长.
如图,AB=AC,DE垂直平分AB,且交AB于点D,交AC于点E.已知BC=2,△BCE的周长为6,求△ABC的周长.